Question #9235b
1 Answer
Mass is the quantity of being. Weight is force.
Explanation:
This is a basic but very important concept in science.
In contrast,
It is measured in
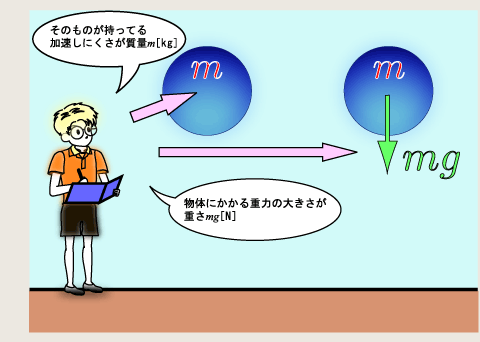
The figure is cited from "質量と重さの違い" by f_master.
http://1st.geocities.jp/f_master001/physics/htmlfile/molarity_and_gravity.html
The Japanese above says that the resistance against acceleration is mass and the gravity force is weight.
Mass of the object does not change no matter where it is put.
Weight of the object is dependent on the place.
For example, assume that I have an object X. Mass of X is
If I were to take it to the moon, where the gravity is about one-sixth times of that of the earth,
However,
For more information:
https://en.wikipedia.org/wiki/Mass_versus_weight

