Let's begin with something easy. You mentioned that you knew how to convert something such as #3^(1/4)# which resulted in #root(4)(3)#.
Looking at #(5ab)^(3/2)#. In radical form this is #(sqrt(5ab))^3#.
How?
Well there is a technique to this.
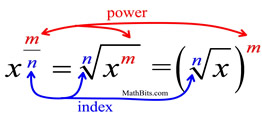
If we apply this to the first example: #3^(1/4)# we can take note that
Power #=color(red)1#
Index#=color(blue)4#
(I color coded to better represent the power and index)
So
#3^(color(red)1/color(blue)4)=(root(color(blue)4)(3))^color(red)1#
Which is simplifies to #root(4)3#
Going back to #(5ab)^(3/2)#, we apply the technique to get
Power#=color(red)3#
Index#=color(blue)2#
So converting into radical form
#(5ab)^(color(red)3/color(blue)2)=(root(color(blue)2)(5ab))^color(red)3#
Which we simplify to #(sqrt(5ab))^3# because #root(2)(5ab)# and #sqrt(5ab)# are the same but it is preferred to not include the #2# because its redundant.
Also, the parenthesis simply indicated that whatever was inside there would go inside the square root. Another example would be #(7a-3b)^(2/5)#. This would mean that #7a-3b# would be inside the square root once we convert it into radical form which eventually is
#(root5(7a-3b))^2#


