There is no temperature at which the mode (most probable), the root mean ssquare velocity (#v_"rms"#) and the average velocity have the same value in m/s.
In fact the probability distribution of molecular velocities (Maxwell distribution) is asymmetric. Look at this one: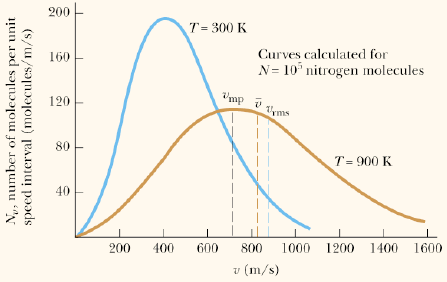
Your teacher should chose one. The easiest one is #v_"rms"#, because, in that case, you could use the simple formula:
#v_"rms" = sqrt((3k_BT)/m)#
where #v_"rms"# is the root mean square velocity in #m/s#;
#k_B# is Botzmann's constant = #1.38064852 × 10^"-23" ""m^2· kg · s^"-2" ·K^"-1"#
#T# is the unknown temperature in kelvin,
#m# is the mass of a dioxygen (#O_2#) molecule in kg.
By assuming 1500 m/s is just the root mean square speed, #v_"rms"#, by using molar mass of dioxygen #(M_(O_2) = 0.031998 "kg"/"mol")#, and knowing that:
#k_B = (R " perfect gas constant")/(N_A " Avogadro's constant")=#
#=(8.31446 " "m^2· kg · s^"-2" ·K^"-1" · mol^"-1")/(6.02214·10^"23"mol^"-1")#,
we can find #T# with the following calculation:
#T=(v_"rms"^2 · M_(O_2))/(3R)=((1500 m/s)^2 · 0.031998 "kg"/"mol")/(3 · 8.31446" "m^2· kg · s^"-2" · K^"-1" · mol^"-1")= 2886 K#
In which I have used the fact that a single dioxygen molecule multiplied by the Avogadro's constant yields the molar mass of dioxigen substance, #M_(O_2) = 0.031998 "kg"/"mol" or 31.998 g/"mol"#.
The most probable speed #v_"mp"#, average speed, #v_"ave"# and the rms speed #v_"rms"# are related in this way:
#v_"mp"=sqrt(3/2) v_"rms"; " "v_"ave"=2/(sqrt(pi))v_"mp"#
I hope this will help you and your teacher.


