Question #e2075
1 Answer
Oct 5, 2017
Point B has the coordinates
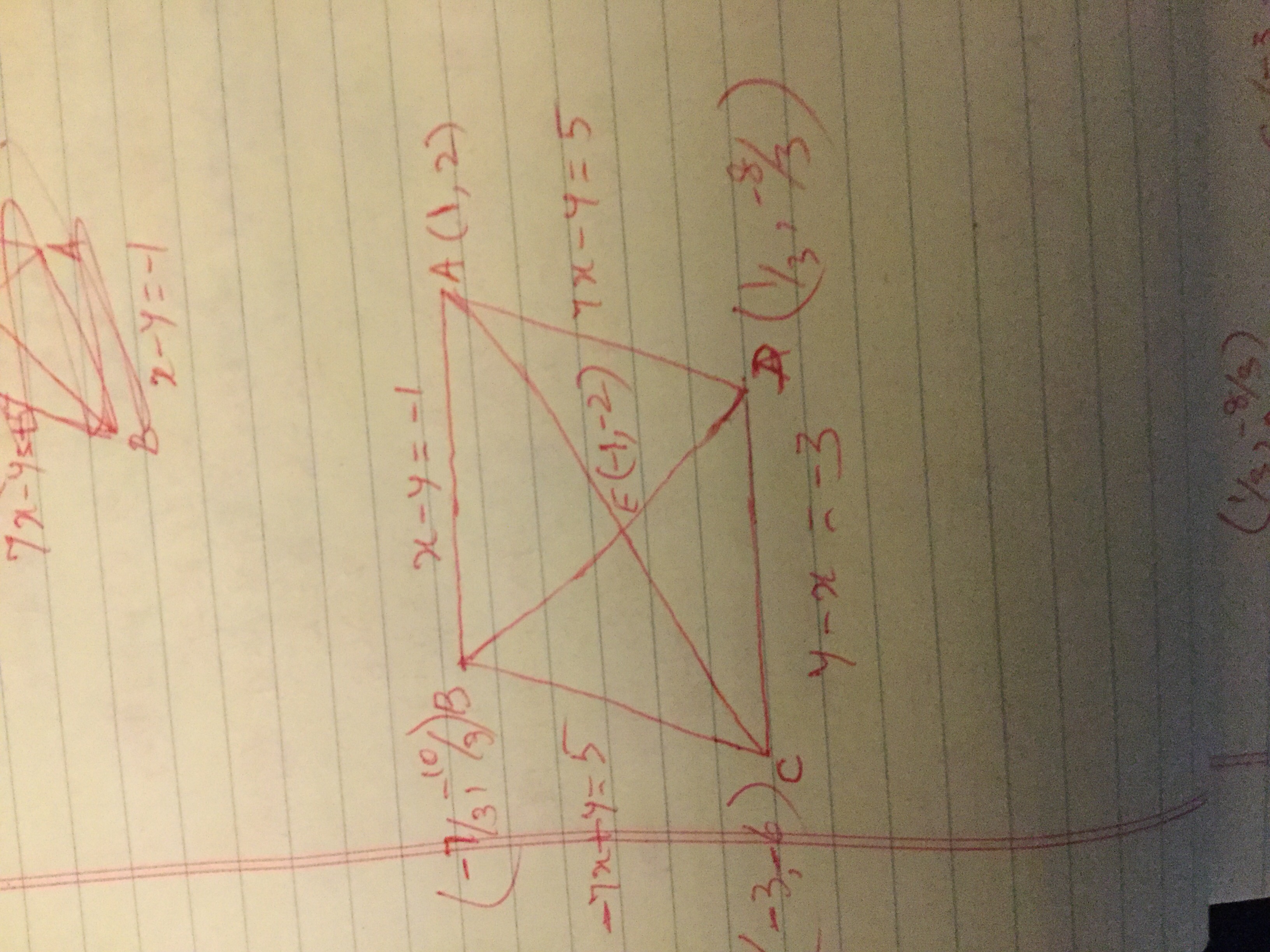
Explanation:
Eqn of line AB is
Eqn of line AD is
Solving Eqn AB & AD, we get point A.
Point A
E is the midpoint of A & C
Point E
Point C
Slope of BC is same as slope of AD
Eqn of line BC is
Solving line Equations AB & BC, we get point B.
Line AB
Line BC
Point B
Slope of CD is same as slope of AB
Eqn of line CD is
Solving Eans AD & CD, we get point D
Line AD
Line CD
Point D
