Question #68d45
1 Answer
Explanation:
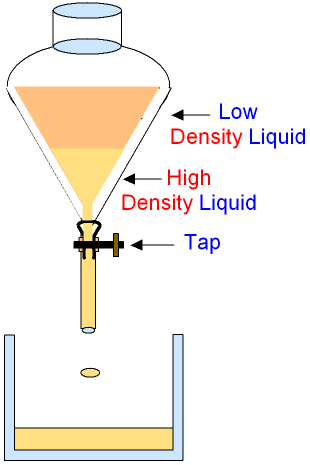 www.gcsescience.com
www.gcsescience.com
In this case the octanol phase is the least dense so this forms the upper layer.
After shaking the propanoic acid distributes itself between the two layers. A dynamic equilibrium is established:
So we can write:
Where p is the partition coefficient.
The total no. of moles of propanoic acid ( which I will shorten to PA) is given by:
During the titration the acid is neutralised:
We can see from this that 1 mole of PA reacts with 1 mole of
This means that the total number of moles of PA in 50 ml of the water phase = 0.00032 x 5 = 0.0016
Since the volumes of both phases are the same we can say:

