Question #9fb71
1 Answer
Explanation:
Parametrization is the process by which one can express a curve in a different space, in function of a single paramater for instance. It is useful in some situations, such as line integration.
From circle to line
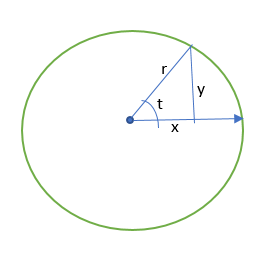
From the circle below, and some trigonometry, we can find the equations:
- x(t) = 1 - cos(t)
- y(t) = 1 - sin(-t) (see that it makes the "clock" goes backwards)
For the initial point, set
- x(t) = 1 - cos(0)=0
- y(t) = 1 - sin(-0)=1
Computer simulation
By using Matlab, we can plot the parametrized curve.
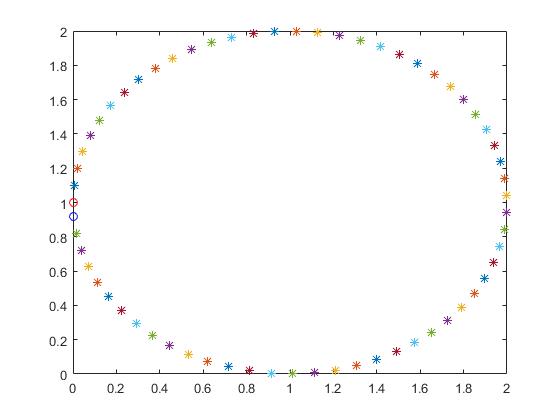
The red circle is the initial point (0,1) and the blue one final; you can show by running the simulation for a small number of points that it is clockwise; furthermore, the only way for the points on the picture is clockwise.
How do you find a parametrized curve?
In order to find a parametrized curve, you must have information about the pathway you want to parametrize, that is what it is for, transforming a function into a space like function. Given the pathway desired, you must have abilities in general with geometry; in general, it is not trivial and may require a "good eye and sense".

