Calculate the length of the arc of # y = 2x-x^2 # for #x in [0,2]?
1 Answer
Arc Length
#~~ 2.970 # to 3dp
Explanation:
Arc Length is given by:
# L = int_alpha^beta \ sqrt(1+(dy/dx)^2) \ dx #
We have:
# y = 2x-x^2 #
Differentiating wrt
# dy/dx = 2-2x #
So the Required Arc Length, is given by:
# L = int_0^2 \ sqrt( 1 + (2-2x)^2 ) \ dx #
# \ \ = int_0^2 \ sqrt( 1 + 4-8x+4x^2 ) \ dx #
# \ \ = int_0^2 \ sqrt( 4x^2-8x+5 ) \ dx #
Now, let us estimate this integral numerically by using the Trapezium rules with
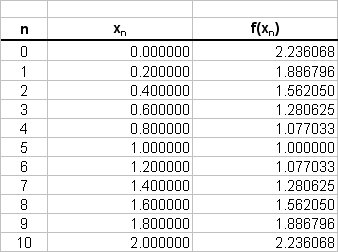
# A = 0.2/2 * { 2.236068 + 2.236068 + #
# \ \ \ \ \ \ \ \ \ 2*(1.886796 + 1.56205 + 1.280625 + 1.077033 + #
# \ \ \ \ \ \ \ \ \ 1 + 1.077033 + 1.280625 + 1.56205 + 1.886796) } #
# \ \ \ = 0.1 * { 4.472136 + 2*(12.613008) } #
# \ \ \ = 0.1 * { 4.472136 + 25.226016 } #
# \ \ \ = 0.1 * 29.698152 #
# \ \ \ = 2.969815 #
So we estimate that:
# L = 2.970 # to 3dp
Actual Value
As it happens this integral can be evaluated and we find that
# L = 1/2(sinh^(-1)(2)+2sqrt(5)) = 2.957885715089195 #

