Question

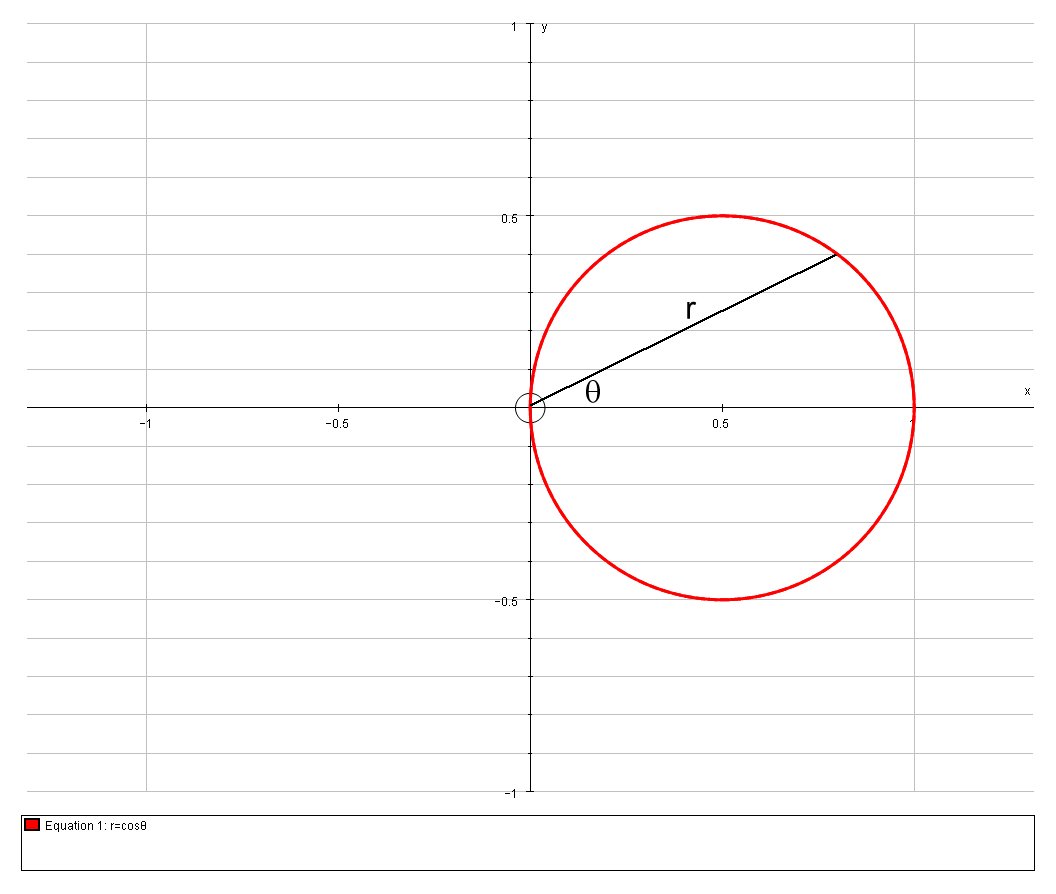
Calculate the area bounded by the polar curve `r=cos theta`?

Answer 1

`pi/4`

Explanation:

`r=costheta`

The area we seek is.

If we convert to Polar Coordinates then the region `R` is:

an angle from `theta=-pi/2` to `theta=pi/2`
a ray from `r=0` to `r=cos theta`

And as we convert to Polar coordinates we get:

`x \ \ \ = rcos theta`
`y \ \ \ = rsin theta`
`dA = dy dy = r dr d theta`

So then the bounded area is given by#

`A = int int_R \ dA`

`\ \ = int_(-pi/2)^(pi/2) \ int_0^(cos theta) \ r dr d theta`

`\ \ = int_(-pi/2)^(pi/2) \ [1/2r^2]_0^(cos theta) \ d theta`

`\ \ = int_(-pi/2)^(pi/2) \ 1/2cos^2theta \ d theta`

`\ \ = int_(-pi/2)^(pi/2) \ 1/2 (1+cos2theta)/2 \ d theta`

`\ \ = 1/4 \ int_(-pi/2)^(pi/2) \ 1+cos2theta \ d theta`

`\ \ = 1/4 \ [theta + (sin2theta)/2]_(-pi/2)^(pi/2)`

`\ \ = 1/4 \ { (pi/2-1) - (-pi/2-(-1)) }`

`\ \ = 1/4 \ ( pi/2-1+pi/2+1)`

`\ \ = 1/4(pi)`

Observations:

Note that `r=cos theta` is the polar equation of a circle of radius `1/2` centred on `(1/2,0)`, hence the area is:

`A = pi(1/2)^2 = pi/4`

Also, note that if we apply the double integration progress to a generic function `r=r(theta)` we get the polar area formula:

`A =int_alpha^beta \ 1/2r^2 \ theta`.