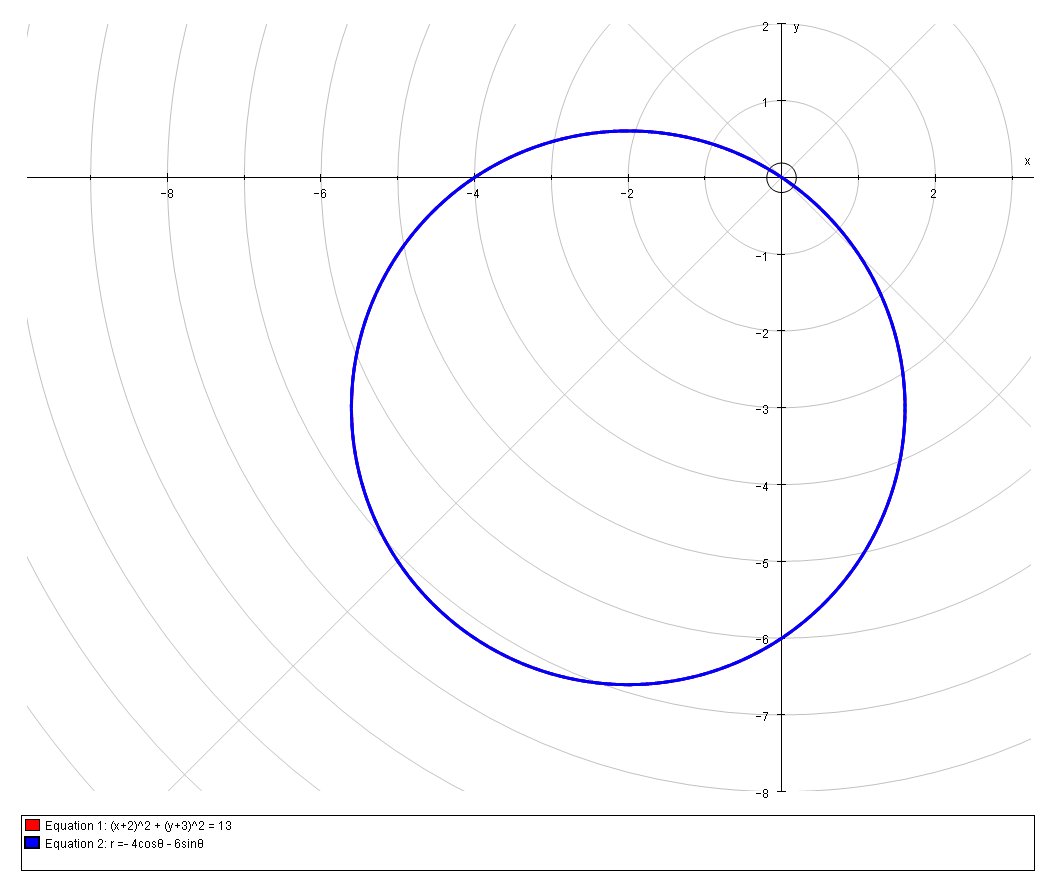
Convert #(x+2)^2 + (y+3)^2 = 13# into polar form?
1 Answer
Oct 30, 2017
# r =- 4costheta - 6sintheta #
Explanation:
Putting:
# x = rcos theta #
# y = rsin theta #
Into the cartesian equation:
# (x+2)^2 + (y+3)^2 = 13 #
we have:
# (rcos theta+2)^2 + (rsin theta+3)^2 = 13 #
# :. r^2cos^2 theta+4rcostheta + 4 + r^2sin^2theta+6rsintheta+9 = 13 #
# :. r^2(cos^2 theta + sin^2theta) + 4rcostheta + 6rsintheta+13 = 13 #
# :. r^2 + 4rcostheta + 6rsintheta = 0 #
# :. r(r + 4costheta + 6sintheta) = 0 #
Leading to two possibilities:
# { (r = 0), (r =- 4costheta - 6sintheta) :}#
Note that the second equation encompases the first when:
# 6sintheta = 4costheta => tan theta = 2/3 #
Hence the Polar equation we seek is:
# r =- 4costheta - 6sintheta #