Question

Question #aff6c

Answer 1

`2.81 * 10^(23)`

Explanation:

The trick here is to realize that each atom of magnesium contributes `2` electrons, its valence electrons, to the "sea of electrons".

The electrostatic force of attraction that exists between the magnesium cations and the sea of electrons is what accounts for the metallic bonding that we see in magnesium.

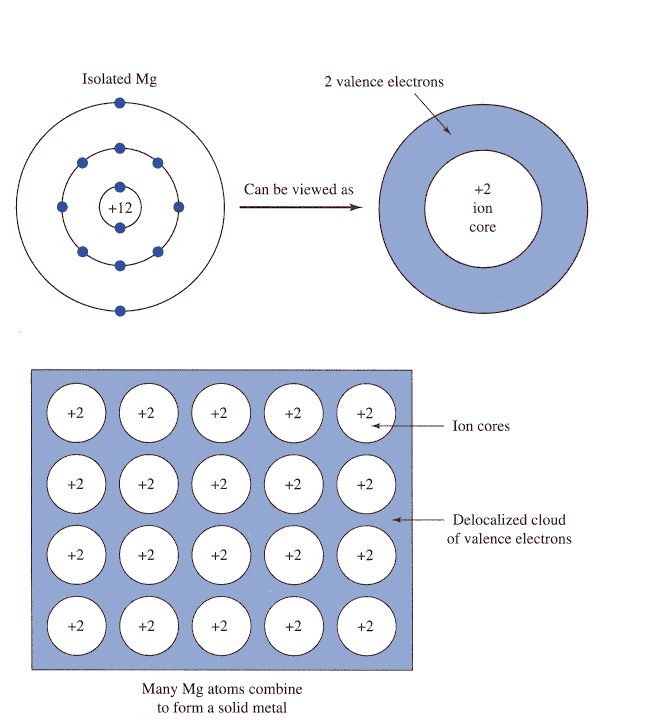
So, your goal here will be to figure out how many atoms of magnesium are present in your sample. To do that, use the molar mass of magnesium to convert the number of grams to moles.

`5.68 color(red)(cancel(color(black)("g"))) * "1 mole Mg"/(24.305color(red)(cancel(color(black)("g")))) = "0.2337 moles Mg"`

Next, use Avogadro's constant, which tells you that in order to have `1` mole of magnesium, you need to have `6.022 * 10^(23)` atoms of magnesium, to convert the number of moles to atoms.

`0.2337 color(red)(cancel(color(black)("moles Mg"))) * (6.022 * 10^(23)color(white)(.)"atoms Mg")/(1color(red)(cancel(color(black)("mole Mg")))) = 1.407 * 10^(23)color(white)(.)"atoms Mg"`

Finally, use the fact that each atom of magnesium donates `2` electrons to the sea of electrons to get

`1.407 * 10^(23)color(red)(cancel(color(black)("atoms Mg"))) * "2 delocalized e"^(-)/(1color(red)(cancel(color(black)("atom Mg")))) = color(darkgreen)(ul(color(black)(2.81 * 10^(23)color(white)(.)"delocalized e"^(-))))`

The answer is rounded to three sig figs, the number of sig figs you have for the mass of magnesium.