First, note that they are asking about the average number of accumulated miles per member, so we can define A(t) = (M(t))/(P(t). Careful consideration will show that this results in a factor of 10^3 (since M(t) is expressed in units of 10^9 while P(t) is expressed in units of 10^6), which is consistent with the statement that A(t) will be represented in thousands.
Now, we can add a third row to the table (if desired) and calculate the value of A(t) for each of these values of t provided by using our formula for A(t):
{:(t, \|, 0 , \|, 2, \|, 4, \|, 6, \|, 8, \|, 10, \|, 12),(P(t), \|, 2, \|, 5, \|, 7, \|, 12, \|, 20, \|, 28, \|, 30), (M(t), \|, 100, \|, 250, \|, 400, \|, 700, \|, 800, \|, 1000, \|, 1700),(A(t), \|, 50, \|, 50, \|, 57.1, \|, 58.3, \|, 40, \|, 35.7, \|, 56.7):}
This provides us with a set of points (t, A(t)) which we can draw as a continuous piecewise function, which looks like this:
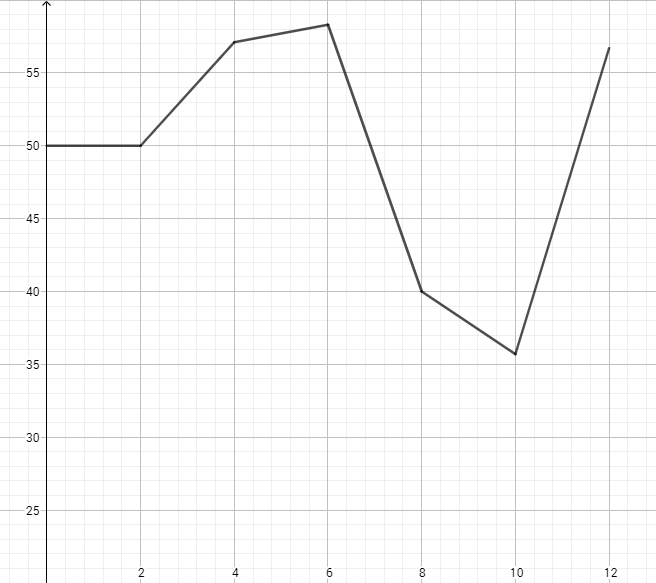
From the piecewise graph, it appears that the function A(t) is hitting a local minimum value around t = 10, which corresponds to the year 1991 (since it was stated that t represents the number of years since 1981.

