The underlying issue you have here is that the inverse cosine function's domain. Consider the graph below:
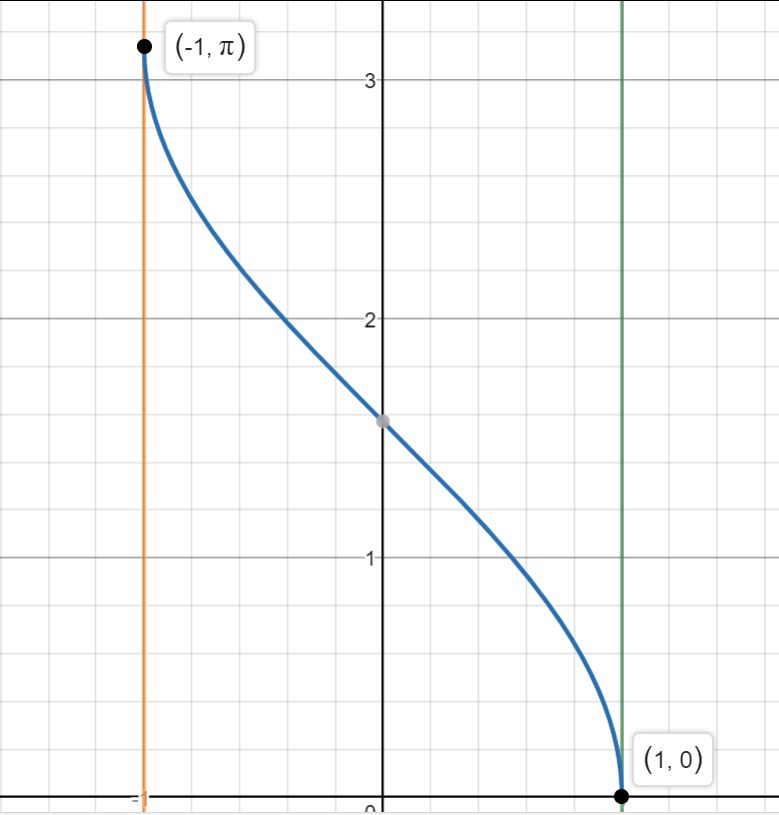
The domain of the #f(x) = cos^-1(x)# is #[-1, 1]# (i.e. all real numbers between #-1# & #1#, inclusive), and the range is #[1, pi]# (i.e. all real numbers between #1# and #pi# inclusive).
Since #2 > 1#, you cannot plug it into the inverse cosine function.
You can also think of why this is not possible using a triangle:
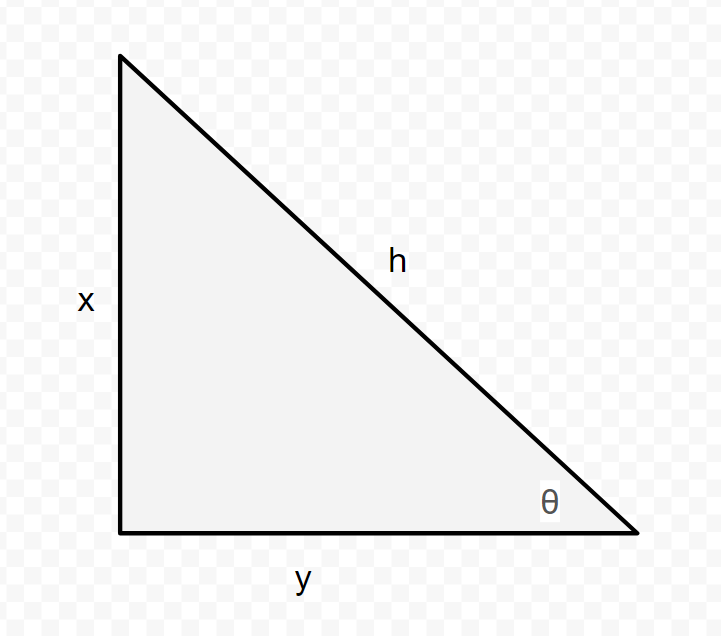
We know that #cos(theta) = y/h#, which means that:
#theta = cos^-1(y/h)#
For #y/h# - the ratio of the length of one side to that of the hypotenuse - to be 2, it implicitly implies that #y > h#, or that that one side is greater in length than that of the hypotenuse. This is not physically possible in a right triangle,
Hope that helped :)

