Question #db4d1
1 Answer
Explanation:
The Rydberg equation allows you to calculate the wavelength,
#1/(lamda) = R * (1/n_f^2 - 1/n_i^2)#
Here
#R# is the Rydberg constant, equal to#1.097 * 10^(7)# #"m"^(-1)#
To find the wavelength of the emitted photon, rearrange the Rydberg equation to solve for
#lamda = (n_i^2 * n_f^2)/(n_i^2 - n_f^2) * 1/R#
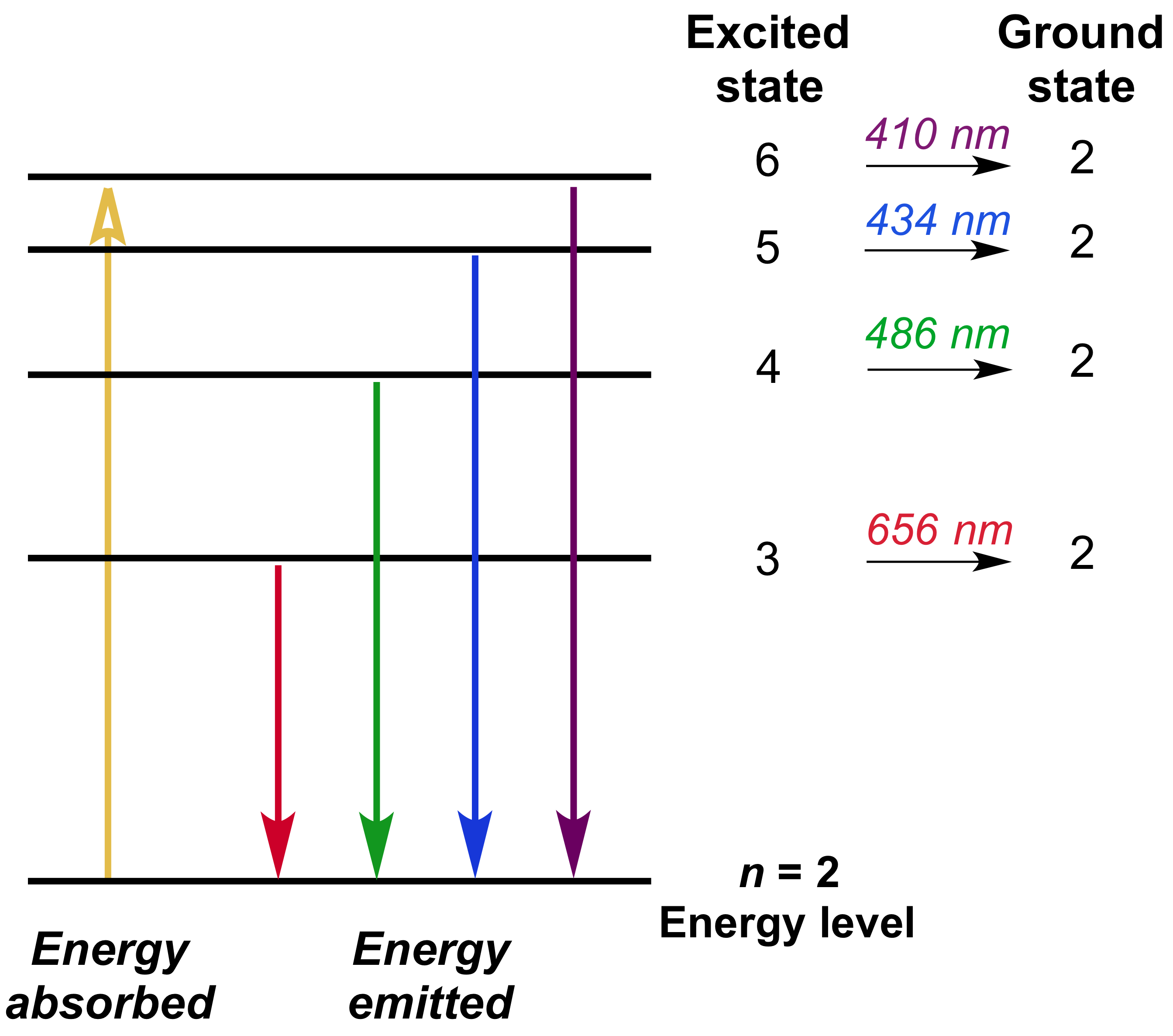
In your case, the electron is going from
#n_i = 6#
to
#n_f = 2#
a transition that is part of the Balmer series, so you should expect the wavelength of the photon to correspond to the visible part of the EM spectrum.
Plug in your values to find
#lamda = (6^2 * 2^2)/(6^2 - 2^2) * 1/(1.097 * 10^(7)color(white)(.)"m"^(-1))#
#lamda = 4.10 * 10^(-7)color(white)(.)"m"#
To convert this to nanometers, use the fact that
#"1 m" = 10^9# #"nm"#
You will end up with
#lamda = 4.10 * 10^(-7)color(red)(cancel(color(black)("m"))) * (10^9color(white)(.)"nm")/(1color(red)(cancel(color(black)("m")))) = color(darkgreen)(ul(color(black)("410 nm")))#
I'll leave the answer rounded to three sig figs.
As you can see, this transition is indeed located in the visible part of the EM spectrum