Question

Question #03297

Answer 1

`n_f = 3`

Explanation:

Your tool of choice here will be the Rydberg equation, which allows you to calculate the wavelength of the photon emitted when an electron in a hydrogen atom makes an `n_i -> n_f` transition.

`1/(lamda) = R * (1/n_f^2 - 1/n_i^2)`

Here

• `R` is the Rydberg constant, equal to `1.097 * 10^(7)` `"m"^(-1)`
• `n_i` is the energy level from which the electron falls
• `n_f` is the energy level to which the electron falls

In your case, you know that the electron falls from the seventh energy level, so

`n_i = 7`

Your goal here is to find the value of the final energy level, `n_f`. Rearrange the Rydberg equation to solve for `n_f`.

`1/lamda = R * (n_i^2 - n_f^2)/(n_i^2 * n_f^2)`

`n_i^2 * n_f^2 = lamda * R * (n_i^2 - n_f^2)`

`n_i^2 * n_f^2 + lamda * R * n_f^2 = lamda * R * n_i^2`

This is equivalent to

`n_f^2 * (n_i^2 + lamda * R) = lamda * R * n_i^2`

which gets you

`n_f = sqrt( (n_i^2 * lamda * R)/(n_i^2 + lamda * R))`

Now all you have to do is to plug in the values that you have--do not forget that the wavelength of the photon must be expressed in meters!

`n_f = sqrt( (7^2 * 1005 * 10^(-9)color(red)(cancel(color(black)("m"))) * 1.097 * 10^7 color(red)(cancel(color(black)("m"^(-1)))))/(7^2 + 1005 * 10^(-9)color(red)(cancel(color(black)("m"))) * 10.97 * 10^7 color(red)(cancel(color(black)("m"^(-1))))))`

`n_f = 2.99983 ~~ 3`

Therefore, you can say that a photon of wavelength `"1005 nM"` is emitted when an electron in a hydrogen atom falls from `n_i = 7` to `n_f = 3`, a transition that is part of the Paschen series.

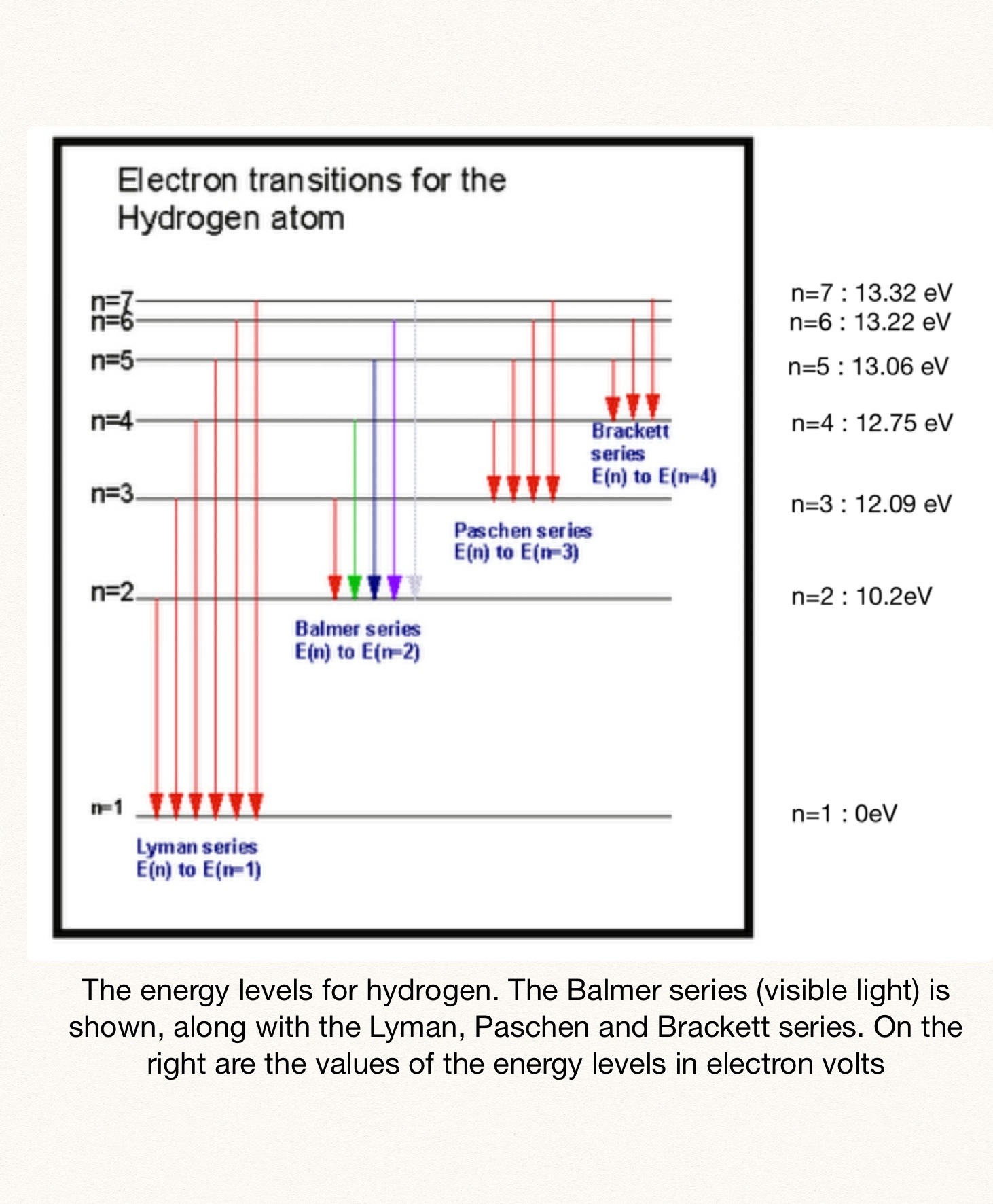https://thecuriousastronomer.wordpress.com/2013/08/20/emission-line-spectra/