The formula for linear least-squares method is
#y-bar y=sigma_(xy)/(sigma_x^2)(x-bar x)#, where
#bar x#, #bar y#: average of #x# and #y#, respectively.
#sigma_x^2#: variance of #x#
#sigma_(xy)#: covarience of #x# and #y#
First, calculate #bar x# and #bar y#.
#bar x=(-2+8+10+15)/4=7.75#
#bar y=(50+75+103+146)/4=93.5#
Then, calculate #sigma_x^2# and #sigma_(xy)#.
#sigma_x^2=((-2-7.75)^2+(8-7.75)^2+(10-7.75)^2+(15-7.75)^2)/4#
#=38.1875#
#sigma_(xy)=((-2-7.75)・(50-93.5)+(8-7.75)・(75-93.5)+(10-7.75)・(103-93.5)+(15-7.75)・(146-93.5))/4#
#=205.375# (sorry for the ugly format!)
Therefore, the formula of the line is
#y-93.5=38.1875/205.375(x-7.75)#
#y-93.5=5.3781(x-7.75)#
#y-93.5=5.3781x-41.680#
#y=5.38x+51.82#
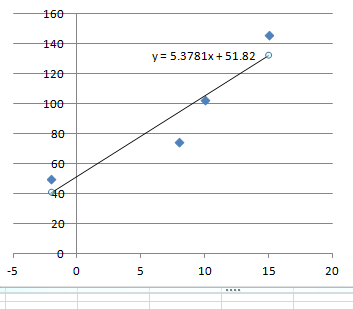
If you can use Microsoft Excel, you can calculate the average,variance and covariance with AVERAGE, VARP and COVAR function, respectively.


