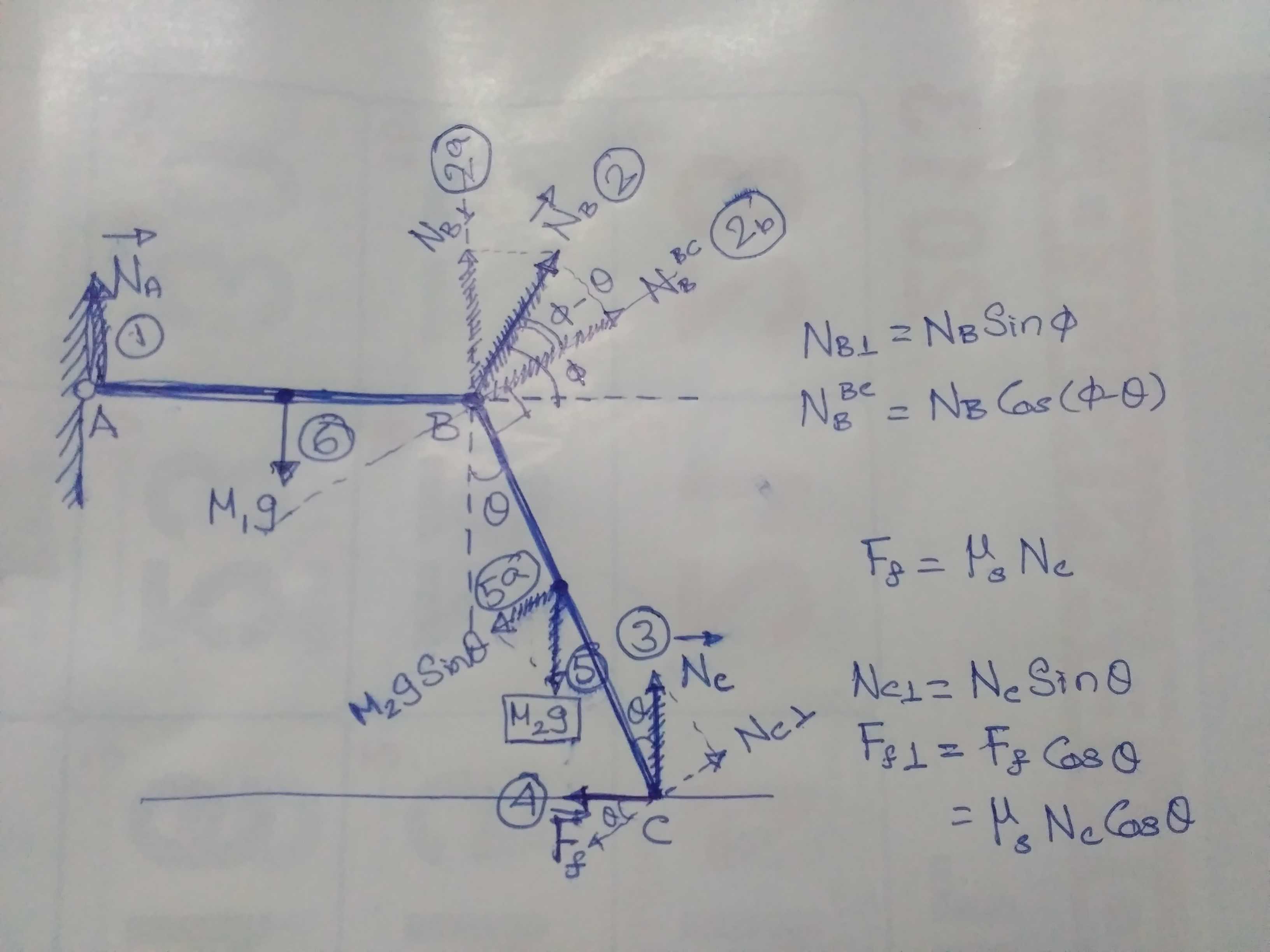
We are going to apply the static equilibrium conditions
(translational equilibrium + rotational equilibrium) to both bars separately.
Translational Equilibrium Condition: #\sum_k vec F_k = vec 0#
Rotational Equilibrium Condition: #\sum_k vec tau = vec 0#
Symbols Used:
#(1) \quad N_A# - Normal force at A ; #\qquad(2) N_B\quad # - Normal force at B;
#(3) \quad N_C# - Normal force at C; #\qquad(4) \quad F_f# - Static friction at C;
#(5)\quad M_2g# - Weight of bar BC; #\qquad (6)\quad M_1g# - Weight of bar AB;
#L# - Length of the bars AB and BC;
Given : #\quad L = 2a; \qquad M_1 = k.m; \qquad M_2 = m#
Situation: The two bars, AB and BC, are hinged at B where their interaction produces a normal force #N_B# that makes an angle #\phi# with respect to the horizontal.
The component of #N_B# responsible for generating a torque on bar AB is : #\quadN_{B_|_} = N_B\sin\phi;\quad# (labeled 2a)
The component of #N_B# responsible for generating a torque on bar BC is: #\quadN_B^{BC} = N_B\cos(\phi-\theta);\quad# (labeled 2b)
[1] Static Equilibrium on Bar AB: Forces acting on this bar are #vec N_A, \quad vec N_B# and #M_1vecg#
[1a] Rotational Equilibrium Condition: Calculating the torques about point A -
#vec \tau_{"net"} = vec \tau_A + vec \tau_g + vec \tau_B#
#vec \tau_{"net"} = +N_A.0 - M_1g(L/2) + N_{B_|_}.L = vec 0#
#N_{B_|_} = (M_1.g)/2# - Thus we get our first unknown.
But, #N_{B_|_} = N_B\sin\phi; \qquad \rightarrow N_B = (M_1.g)/(2\sin\phi)# ...... (EQ1)
[1b] Translational Equilibrium Condition: Vector sum of all the forces acting on bar AB must vanish.
#vec F_{"net"} = vec F_A + vec F_g + vec F_B = vec 0;#
Vertical Component: #\qquadN_A - M_1g + N_{B_|_} = 0#
#N_{A} = M_1.g - N_{B_|_} = M_1.g - (M_1.g)/2 = (M_1.g)/2#
[2] Static Equilibrium Condition on Bar BC: Forces acting on this bar are #vec N_B, \quad vec N_C, \quad M_2.vecg,# and #vec F_f#.
[2a] Rotational Equilibrium Condition: Calculating the torques about point C,
#vec \tau_{"net"} = vec \tau_B + vec \tau_g + vec \tau_C + vec \tau_f = vec 0;#
#vec \tau_{"net"} = -N_B^{BC}.L + M_2.g\sin\theta(L/2) + (F_f-N_{C_|_}).0 = vec 0#
#N_B^{BC} = (M_2.g\sin\theta)/2; \qquad \rightarrow N_B\cos(\phi-\theta) = (M_2.g\sin\theta)/2#
#N_B = (M_2.g\sin\theta)/(2\cos(\phi-\theta))# ...... (EQ2)
Comparing (EQ1) and (EQ2) we can get,
#(M_1.g)/(2\sin\phi) = (M_2.g\sin\theta)/(2\cos(\phi-\theta))#
#M_1/M_2 = (\sin\theta\sin\phi)/(\cos(\phi-\theta)) = (\sin\theta\sin\phi)/(\cos\theta\cos\phi + \sin\theta\sin\phi) = 1/(1+\cot\theta\cot\phi)#
#\cot\phi = (M_2/M_1-1)\tan\theta = -2/(3\sqrt{3}); \qquad \phi = 68.9^o#
Because, #M_1 = k.m = 3m; \qquad M_2 = m; \qquad \theta = 30^o#
[2b] Translational Equilibrium Condition: Vector sum of all the forces acting on bar BC must vanish.
#vec F_{"net"} = vec F_B + vec F_g + vec F_C + vec F_f = vec 0;#
Vertical Component: #\qquadN_{B_|_} - M_2g + N_{C} = 0#
#N_C = M_2.g - N_{2_|_} = M_2.g - N_2\sin\phi #
#N_C = M_2.g - (M_1.g)/(2\sin\phi).\sin\phi = (M_2-M_1/2)g# ...... (EQ3)
Calculating Friction Coefficient:
Now to find the frictional force apply the rotational equilibrium condition again, BUT this time calculating the torques about point B.
Rotational Equilibrium Condition (Again): Calculating the torques about point B,
#vec \tau_{"net"} = vec \tau_B + vec \tau_g + vec \tau_C + vec \tau_f = vec 0;#
#0 = N_{B_|_}.0-M_2.g\sin\theta.(L/2)+(N_C\sin\theta-F_f\cos\theta).L#
#(M_2.g\sin\theta)/2 = N_C\sin\theta - F_f\cos\theta = N_C\sin\theta - \mu_sN_C\cos\theta#
#(M_2.g)/2 = N_C(1-\mu_s/\tan\theta); \qquad \mu_s = \tan\theta(1-(M_2.g)/(2N_C))#
Using (EQ3) replace #N_C# in the expression for #\mu_s#,
#\mu_s = \tan\theta(1 - (M_2.g)/(2(M_2-M_1/2)g)) = \tan\theta(1-(M_2)/(2M_2-M_1))#
#M_1 = 3m; \qquad M_2 = m; \qquad \theta = 30^o#
#\mu_s=2\tan30^o = 2\times\sqrt{3}/2 = \sqrt{3}#