.
The equation of ellipse can be turned into:
#x^2/a^2+y^2/b^2=1#
#(b^2x^2+a^2y^2)/(a^2b^2)=1#
#b^2x^2+a^2y^2=a^2b^2#
#a^2y^2=a^2b^2-b^2x^2#
#y^2=(a^2b^2-b^2x^2)/a^2#
#y=sqrt((a^2b^2-b^2x^2)/a^2)#
The equation of the line is:
#y=mx+c#
To find the intersection points we set the two equations equal to each other and get an equation in terms of #x#:
#sqrt((a^2b^2-b^2x^2)/a^2)=mx+c#
#(a^2b^2-b^2x^2)/a^2=(mx+c)^2#
#(a^2b^2-b^2x^2)/a^2=m^2x^2+2cmx+c^2#
#a^2b^2-b^2x^2=a^2m^2x^2+2a^2cmx+a^2c^2#
#a^2b^2-b^2x^2-a^2m^2x^2-2a^2cmx-a^2c^2=0#
#(-b^2-a^2m^2)x^2-2a^2cmx+a^2b^2-a^2c^2=0#
This is a quadratic equation with the variable #x# in standard form:
#ax^2+bx+c=0#
To solve for #x#, we need to use the quadratic formula:
#x=(-b+-sqrt(b^2-4ac))/(2a)#
For the line to touch the ellipse, it would have to have only one intersection point with it. This means that our quadratic equation has to have only one answer for #x#.
This happens when the discriminant is equal to zero, i.e.:
#b^2-4ac=0#
In our problem:
#a=-b^2-a^2m^2#
#b=-2a^2cm#
#c=a^2b^2-a^2c^2#
Therefore, the discriminant is:
#(-2a^2cm)^2-4(-b^2-a^2m^2)(a^2b^2-a^2c^2)=0#
#4a^4c^2m^2-4(-a^2b^4+a^2b^2c^2-a^4b^2m^2+a^4c^2m^2)=0#
#4a^4c^2m^2+4a^2b^4-4a^2b^2c^2+4a^4b^2m^2-4a^4c^2m^2=0#
#4(a^4c^2m^2+a^2b^4-a^2b^2c^2+a^4b^2m^2-a^4c^2m^2)=0#
#a^4c^2m^2+a^2b^4-a^2b^2c^2+a^4b^2m^2-a^4c^2m^2=0#
#cancelcolor(red)(a^4c^2m^2)+a^2b^4-a^2b^2c^2+a^4b^2m^2cancelcolor(red)(-a^4c^2m^2)=0#
#a^2b^4-a^2b^2c^2+a^4b^2m^2=0#
#a^4b^2m^2=a^2b^2c^2-a^2b^4#
#a^4b^2m^2=a^2b^2(c^2-b^2)#
#m^2=(a^2b^2(c^2-b^2))/(a^4b^2#
#m^2=(c^2-b^2)/a^2#
#m=+-sqrt(c^2-b^2)/a#
This is the condition that we have to have in order for the line to touch the ellipse, i.e., its slope #m# has to be equal to #+-sqrt(c^2-b^2)/a.#
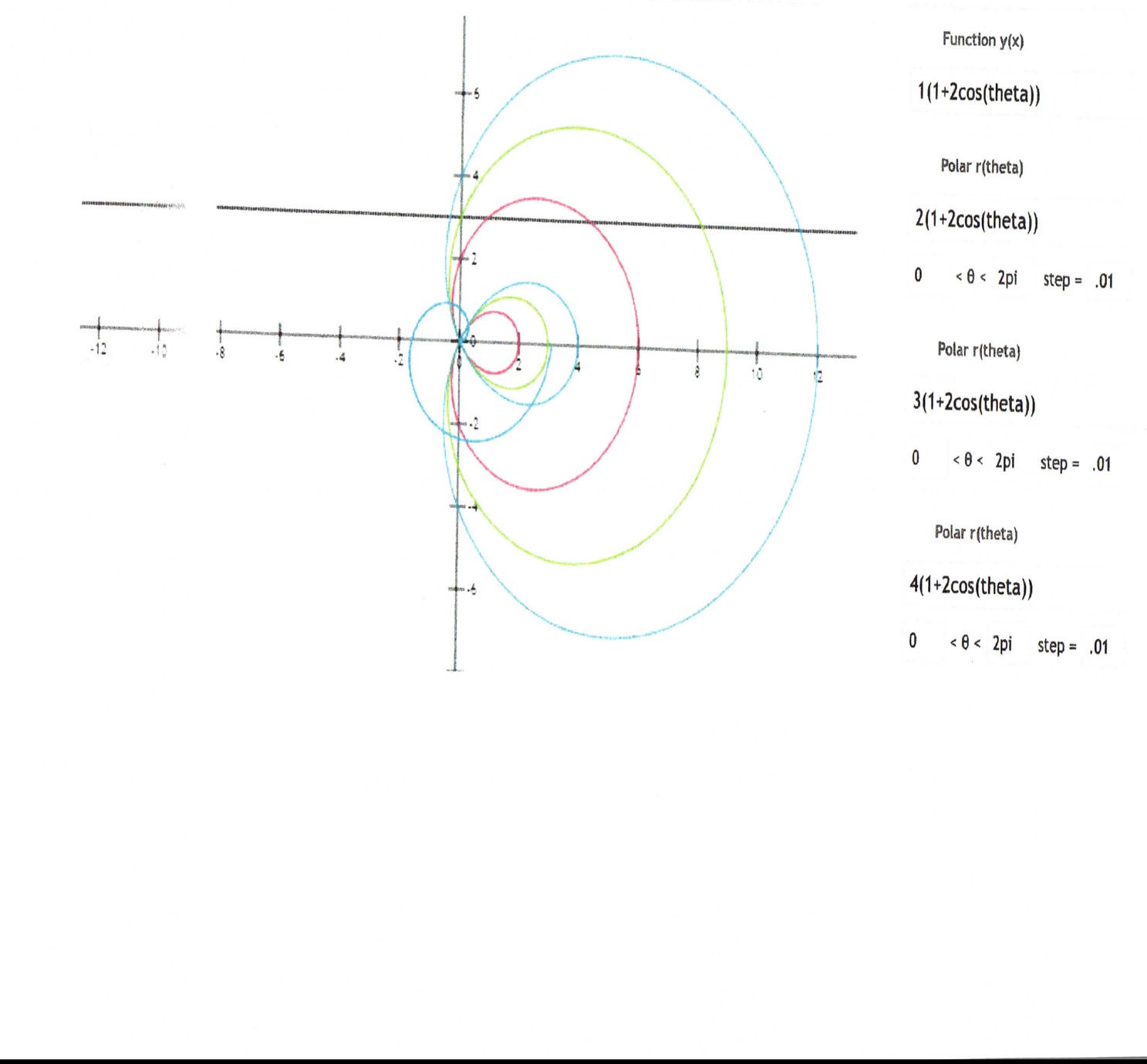
As far as the sketch of the curve of #r=a(1+2costheta)#, the following shows the graphs of this curve for 4 different values of #a#.
#a=1# is the first blue curve (small one)
#a=2# is the red curve
#a=3# is the green curve
#a=4# is the blue curve (large one)
#a# can have any value. As such, you can have infinite curves.