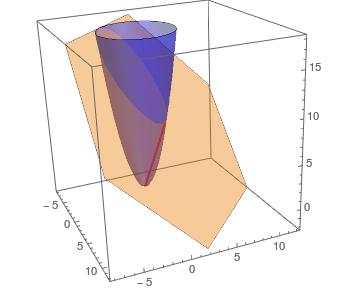
Distance on parabola: The distance of any arbitrary point on the parabola #z=x^2+y^2# is
#S(x,y) = \sqrt{x^2+y^2+z^2(x,y)}=\sqrt{x^2+y^2+(x^2+y^2)^2}#
#\qquad \qquad \qquad = \sqrt{(x^2+y^2)(1+x^2+y^2)}# ...... (Eq 1)
This is the function in whose extremum we are interested in
Constraint Condition: But we do not consider all the points on the parabola but only those points that lie on the intersection with the plane #x+y+z=12#.
Plane: #\quad z = 12 - (x+y)#
Parabola: #\quad z = x^2+y^2#
To find the equation representing the locus of intersection points, eliminate #z# in the parabola equation using its value on the plane equation,
#(x^2+y^2)=12-(x+y); #
#x^2+y^2+(x+y)-12=0# ......(Eq 2)
So #x# and #y# cannot take arbitrary values but are subjected to a further constraint given by Eq 2. The constraint function is then #\phi(x,y) = x^2 + y^2 + (x+y) - 12#;
Lagrange Multiplier Technique: When you want to extremize a function #S(x,y)# subject to the constraint #\phi(x,y)=0#, define a new function #\L(x,y) = S(x,y) - \lambda\phi(x,y)#. This new function #L(x,y)# is the Lagrangian and #\lambda# is the Lagrangian Multiplier. Extremizing the Lagrangian #L(x,y)# is equivalent to extremizing #S(x,y)#, subject to the constraint #\phi(x,y)=0#.
Applying this technique to our problem -
Step 1: Construct the Lagrangian function and calculate its gradient,
#L(x,y) = S(x,y) - \lambda\phi(x,y);#
#S(x,y) = \sqrt{(x^2+y^2)(1+x^2+y^2)};#
#\phi(x,y) = (x^2+y^2)+(x+y)-12;#
#\frac{\delS}{\delx} = \frac{x{1+2(x^2+y^2)}}{\sqrt{(x^2+y^2)(1+x^2+y^2)}};#
#\frac{\delS}{\delx} = \frac{y{1+2(x^2+y^2)}}{\sqrt{(x^2+y^2)(1+x^2+y^2)}};#
#\frac{\del\phi}{\delx} = (2x+1); \qquad \qquad
\frac{\del\phi}{\delx} = (2x+1); #
#\gradL(x,y) = \frac{\delL}{\delx}\hati + \frac{\delL}{\dely}\hatj;#
#\frac{\delL}{\delx} = \frac{\delS}{\delx} - \lambda\frac{\del\phi}{\delx}; \qquad \qquad
\frac{\delL}{\dely} = \frac{\delS}{\dely} - \lambda\frac{\del\phi}{\dely}; #
Step 2: The extremum points of the Lagrangian is found by setting its gradient to zero and solve the set of equations that each component of the gradient yields,
#\gradL(x,y) = 0; \qquad \frac{\delL}{\delx}=0; \qquad \qquad \frac{\delL}{\dely}=0#
Step 3: Solve these equations to find the coordinates of the extremum point.
X component:
#\quad \frac{\delS}{\delx} - \lambda\frac{\del\phi}{\delx}=0; \qquad \rightarrow \qquad \frac{\delS}{\delx} = \lambda\frac{\del\phi}{\delx};#
#\frac{x{1+2(x^2+y^2)}}{\sqrt{1+(x^2+y^2)}} = \lambda(2x+1)#
#\lambda = (\frac{x}{2x+1})(\frac{1+2(x^2+y^2)}{\sqrt{1+x^2+y^2}})# ...... (Eq 3)
Y component:
#\frac{\delS}{\delx} - \lambda\frac{\del\phi}{\delx}=0; \qquad \rightarrow \qquad \frac{\delS}{\delx} = \lambda\frac{\del\phi}{\delx};#
#\frac{y{1+2(x^2+y^2)}}{\sqrt{1+(x^2+y^2)}} = \lambda(2y+1)#
#\lambda = (\frac{y}{2y+1})(\frac{1+2(x^2+y^2)}{\sqrt{1+x^2+y^2}})# ...... (Eq 4)
Eliminating #\lambda# between Eq 3 and Eq 4,
#(\frac{x}{2x+1}) = (\frac{y}{2y+1}) \qquad \rightarrow \qquad x(2y+1)=y(2x+1)#
#cancel{2xy} + x = cancel{2xy} + y; \qquad x = y#
Lagrangian #L(x,y)# has an extremum along the #x=y# plane,
Step 4: Evaluate the complete set of the coordinates, using the constraint equation,
Substituting this (#x=y#) in the constraint equation #\phi(x,y)=0#, we get
#2x^2+2x-12=0; \qquad \rightarrow \qquad x^2+x-6=0#
This quadratic equation has solutions : #x_1=+2; \qquad x_2=-3;#
#x_1=+2# is the meaningful solution.
At #(x,y)=(2,2)# the value of #z# is found either by using the plane equation or by using the parabola equation. Alternatively, we can use both and verify that they both result in the same value.
Parabola: #x^2+y^2=z; \qquad z = 2^2+2^2=8;#
Plane: #z = 12-(x+y)=12-(2+2)=8;#
Thus the Lagrangian #L(x,y)# shows that the extreme value is at #(x,y,z)=(2,2,8)#.
It lies at a distance of
#S(x=2,y=2) = \sqrt{(2^2+2^2)(1+2^2+2^2)} = 6\sqrt{2}# units from the coordinate origin.