Question #63413
1 Answer
The question itself has a number of issues in it:
- Speed does not change at all in uniform circular motion.
- You cannot have uniform (or any kind of) circular motion without a force.
Explanation:
There are a couple of things inherently wrong with the problem statement.
Firstly, by definition, uniform circular motion means that the object is moving in a circle at a constant speed. This essentially means that if what you have is uniform circular motion, the speed of your object will not change!
What does change, however, is the tangential velocity of the object. This is since velocity is a vector quantity, it has both magnitude and direction. While moving in a circle, the object will keep changing direction (even if its speed is constant), which means that the velocity is also changing.
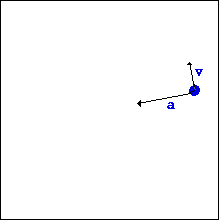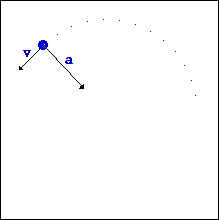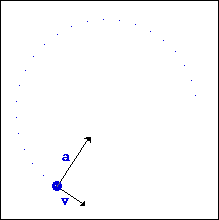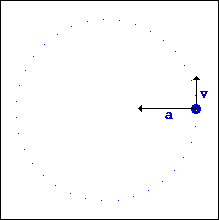
Now, consider this: if an object's velocity is changing, then it must, by definition, be accelerating. What causes an acceleration? A force! Therefore, you must have a force acting on your object for it to have any kind of circular motion.
Does this mean that the problem statement is wrong? Yes....and no. Yes, since it is inherently impossible to have circular motion without some force present, but no since you typically do not use the
What you use is called the radial & tangential (sometimes
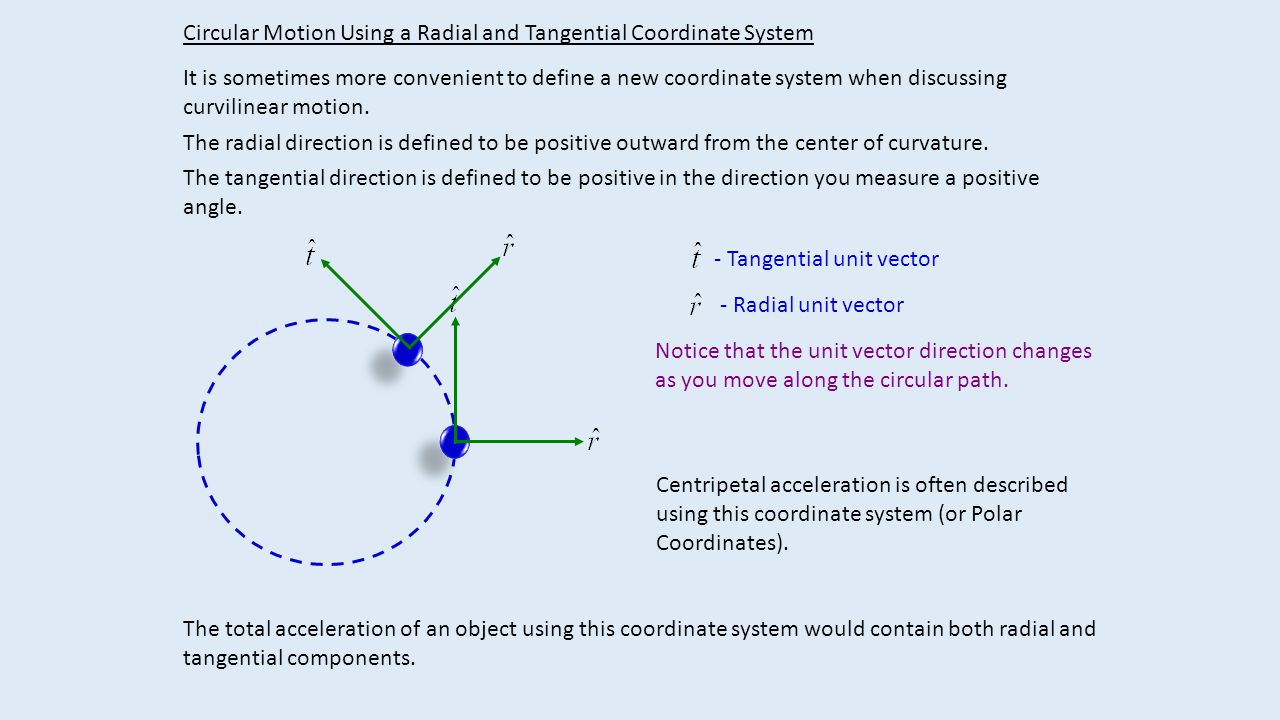
You must have some force acting on the
So, to summarize:
- Speed is constant in uniform circular motion.
- Velocity, however, is not, since you are constantly changing direction.
- This means you must have some force acting on your object for it to have uniform (or any kind of) circular motion.
- This force must be pointing towards the center of the circle.
Hope that helped :)

