Question #8a062
1 Answer
I got
Explanation:
Here
Ampère's law gives the magnetic field (magnetic flux density) inside a solenoid as
#color(blue)(vecB=munIhatz)# (for a solenoid positioned vertically)
where:
#mu# is the magnetic permeability constant#n# is the turn density#N//L# #I# is the current running through the solenoid
Note that the magnetic field outside of the solenoid is
We are given that
#B=4pixx10^(-7)*75/0.01*0.25#
#=0.00235619" T"#
#=>color(blue)(B~~2.4xx10^-3" T ")# or#" "2.4xx10^-3 "Wb"//"m"^2#
The magnetic flux is then given by
#color(Blue)(phi=intvecB*dveca)#
Here, the area of concern is the cross-sectional area of the solenoid. You can either do the integral or just treat it like
#phi=Bint_0^(2pi)int_0^(0.03)(r)drdphi#
Note that
#phi=B*2pi*1/2*r^2|_0^(0.03)#
#=>phi=(0.00235619)*pi(0.03)^2#
#=>color(blue)(phi=6.7xx10^-6"Wb")#
Magnetic field/flux density of a solenoid:
Consider a very long solenoid, consisting of
From the right hand rule, we expect that the magnetic field points upward inside the solenoid and downward outside.
Apply Ampère's law to two rectangular loops:
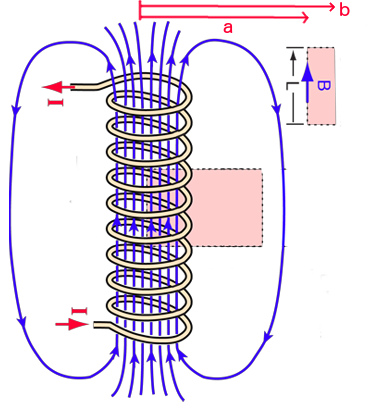
Loop 1 lies entirely outside the solenoid, with its sides at distances
#oint" "vecB*dvecl#
#=[B(a)-B(b)]L#
#=mu_0I_"enc"#
#=0#
Where
Then is follows that
This indicates that the field outside of the solenoid does not depend on the distance from the axis. However, we know that the field must go to zero very far away from the solenoid. Therefore, it must be the case that the field is zero everywhere outside of the solenoid. Clever!
As for loop 2, which is half inside and half outside of the solenoid, Ampère's law gives:
#oint" "vecB*dvecl=BL#
#=mu_0I_"enc"#
#=mu_0nIL#
Hence, the magnetic field inside of a solenoid is given by

