Question

Question #54360

Answer 1

I get answer A.

Explanation:

Here is a force diagram of the situation:

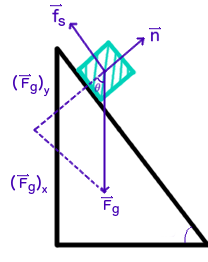
We can use this to come up with statements of the net force. Let's define up the ramp as the positive direction.

`sumF_"x"=f_s-F_"Gx"=ma_x`

`sumF_"y"=n-F_"Gy"=ma_y`

We know that there is no acceleration in the y-direction (the block does not move up or down relative to the surface of the ramp), so we have:

`n=F_"Gy"`

Using trigonometry, we see that the x-component of the gravitational force `F_"Gx"` is found using the sine function (see diagram).

`sin(theta)=(F_"Gx")/F_G`

`=>F_"Gx"=F_Gsin(theta)`

And similarly `F_"Gy"=F_Gcos(theta)`

Then we know that `F_G=mg`, so we may write:

`color(blue)(F_"Gx"=mgsin(theta))`

`color(blue)(F_"Gy"=mgcos(theta))`

Then:

`f_s-mgsin(theta)=ma_x`

Since we've established that there is no acceleration in the y-direction, all acceleration must be in the x-direction. We can solve for `a_x`:

`a_x=(f_s-mgsin(theta))/m`

We also know that `f_"smax"=mu_sn`, or `f_"smax"=mu_smgcos(theta)`, since we established above that `n=F_"Gy"`. Substituting this in, we get:

`a_x=(mu_smgcos(theta)-mgsin(theta))/m`

Then we can factor out an cancel `m`:

`a_x=(cancelm(mu_sgcos(theta)-gsin(theta)))/cancelm`

`=>a_x=mu_sgcos(theta)-gsin(theta)`

`=>color(blue)(a_x=g(mu_scos(theta)-sin(theta)))`

We are given:

• `mu_s=1/sqrt3`
• `theta=30^o`

So we can now solve for `a_x`:

`a_x=(9.81"m"//"s"^2)(1/sqrt3cos(30^o)-sin(30^o))`

Where `cos(30^o)=sqrt3/2` and `sin(30^o)=1/2`

`=>a_x=(9.81"m"//"s"^2)(1/sqrt3*sqrt3/2-1/2)`

`=>a_x=(9.81"m"//"s"^2)(1/2-1/2)`

`=>a_x=0" m"//"s"^2`