Question

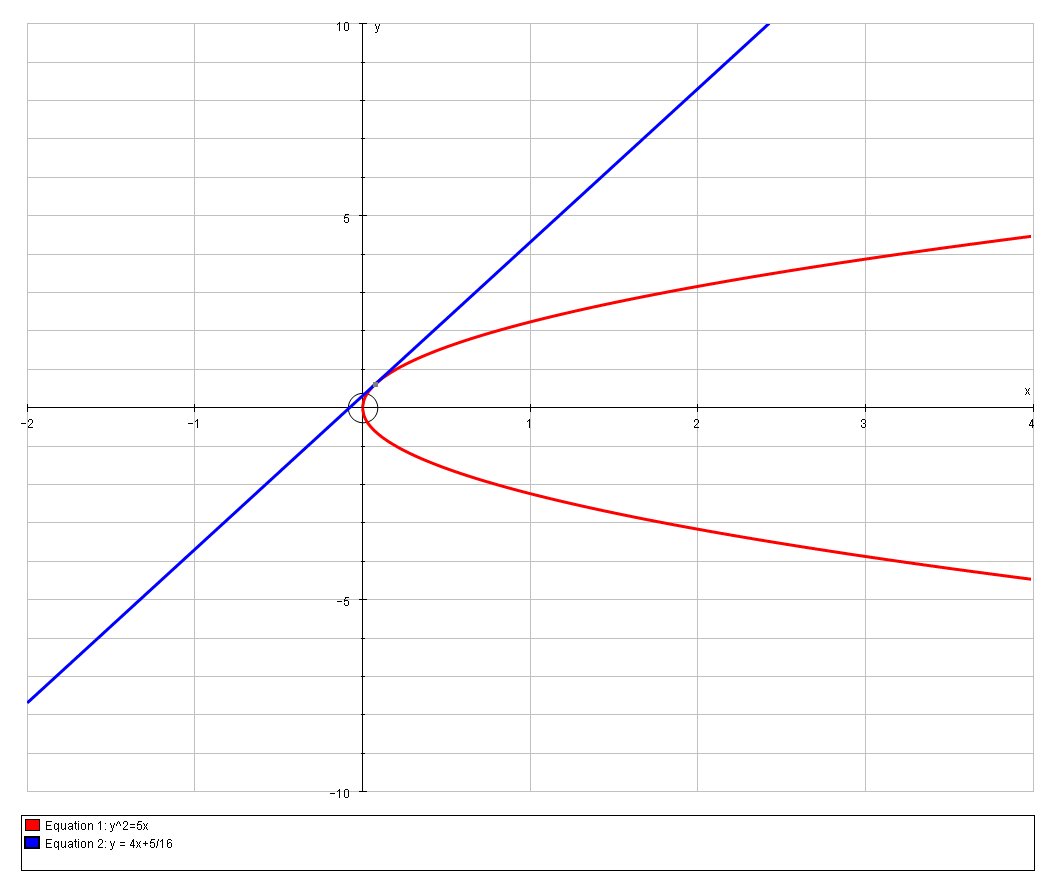
Find the equation of the tangent to the Parabola `y^2=5x`, that is parallel to `y=4x+1` which meets the Parabola at the coordinate `(5/64,5/8)`?

Answer 1

The tangent to the Parabola that is parallel to `y=4x+1` is:

`y = 4x+5/16`

Which meets the Parabola at the coordinate:

`(5/64,5/8)`

Explanation:

We have a parabola given by:

`y^2=5x`

graph{y^2=5x [-5, 5, -5, 5]}

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. So if we differentiate the parabola equation (implicitly) we have:

`2y dy/dx = 5 => dy/dx = 5/(2y)`

Comparing the given line equation `y=4x+1` with the standard line equation `y=mx+x` we see that its gradient is given by:

`m=4`

So we seek a tangent equation for the parabola with the same slope, thus we require:

`dy/dx =4 => 5/(2y) = 4 => y=5/8`

When `y=5/8` the corresponding `x`-coordinate is given by:

`y^2=5x => 5x=25/64 => x = 5/64`

So the point of contact is `(5/64,5/8)`. So, using the point/slope form `y-y_1=m(x-x_1)` the tangent equations is;

`y-5/8 = 4(x-5/64)`
`:. y-5/8 = 4x-5/16`
`:. y = 4x+5/16`