Question #e2d7d
2 Answers
See below.
Explanation:
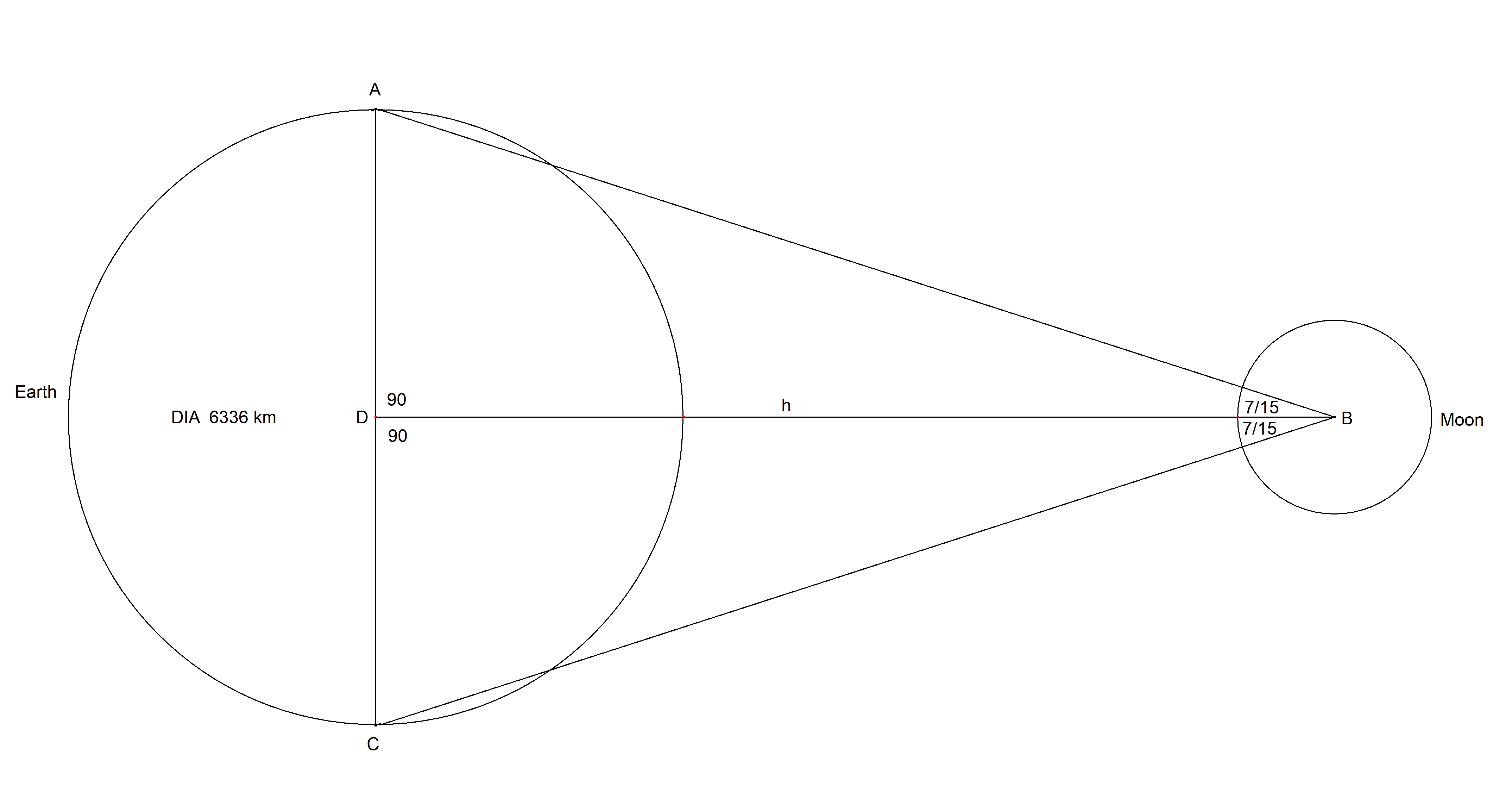
From the diagram we can see that
We seek distance DB
This is the distance to the centres.
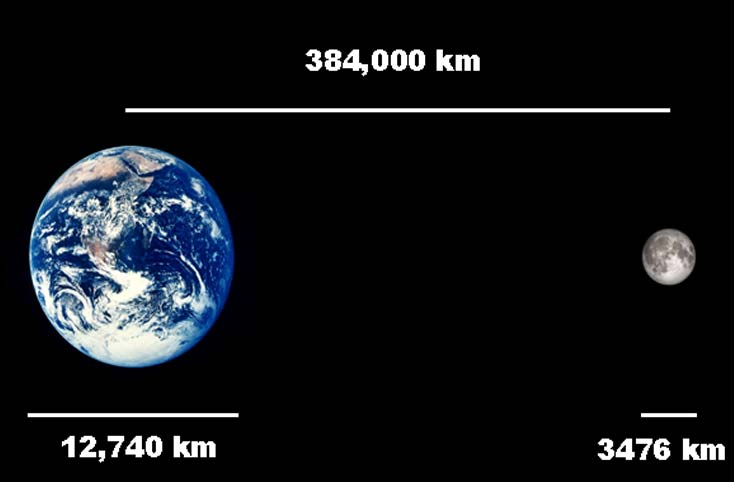
The true distance of the Earth from the Moon is 384,400 km. This is close considering the true diameter of the Earth is 12,742 km and not 6336 km.
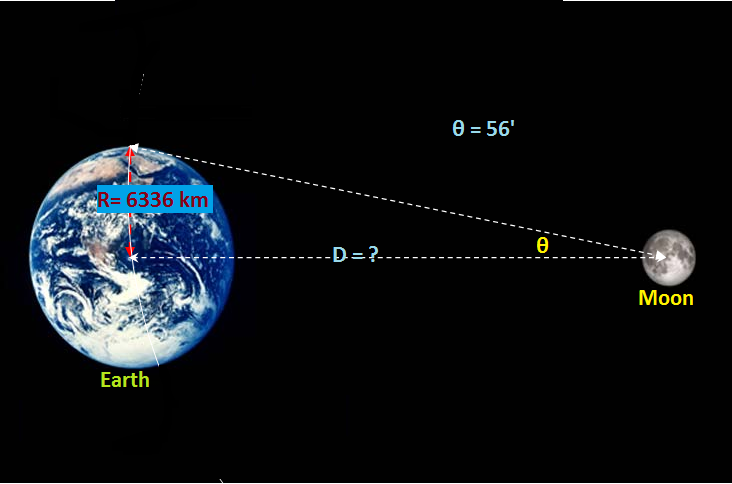
Comparing with the available data of radius of the earth I assume that earth's radius
So we can write
Transforming the angle in radian
So we get
( It is comparable to available figure as shown below)