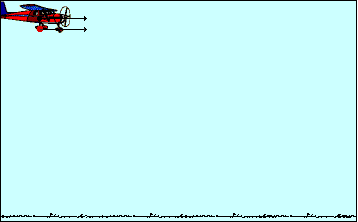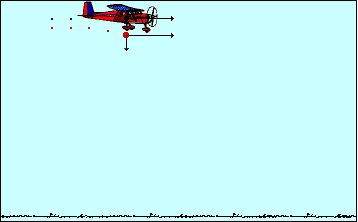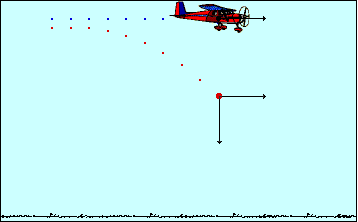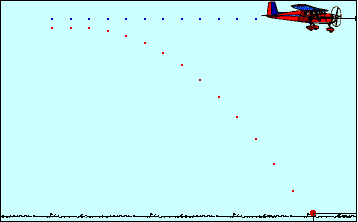
Question

Question #9add1

Answer 1

A kinematics question (or SUVAT question) is always answered in the same way ...

Explanation:

Provided acceleration is constant (like it is here) we can just use a simple 3 step method. Note I use the convention: s (m) for displacement, u (m/s) for initial velocity, v (m/s) for final velocity, a (`m/s^2`) for acceleration and t for time.

Step 1:
Write down the variables with their values & units. Put a question mark next to the one you need to find. Use a dash for the variable that isn’t mentioned / sought.

s = ? m
u = 0 m/s (plane was horizontal)
v = -
a = 9.81 `m/s^2`
t = 9 s

Step 2:
Select the equation that ‘misses out’ your irrelevant variable, rearrange so your unknown is the subject of the equation (on its own on the LHS of the equality)

In this case it must be `s = u.t + 1/2at^2` and note that because u = 0 this means u.t = 0 so we get:

`s = 1/2at^2`

Step 3:

Insert values and find an answer, not forgetting the units.

`s = 1/2xx9.81xx(9^2)`

`s = 397`m

Given the precision of the data (1 s.f.) I think 400m would be a better answer.

Answer 2

Here's what I got.

Explanation:

The trick here is to realize that the fact that the plane is moving horizontally does not impact the time needed for the packet to reach the ground.

In other words, the packet would reach the ground in the exact same time if dropped from a stationary point located at the same height as the plane.

The horizontal movement of the plane will affect where the package will hit the ground, but not when.

This basically means that the vertical component of the velocity with which the package hits the ground when launched from a plane that's moving horizontally will be equal to the velocity with which the package would hit the ground if we were to drop it from rest from a height `h`.

This basically means that the velocity of the plane in the horizontal direction does not affect the time needed for the package to hit the ground.

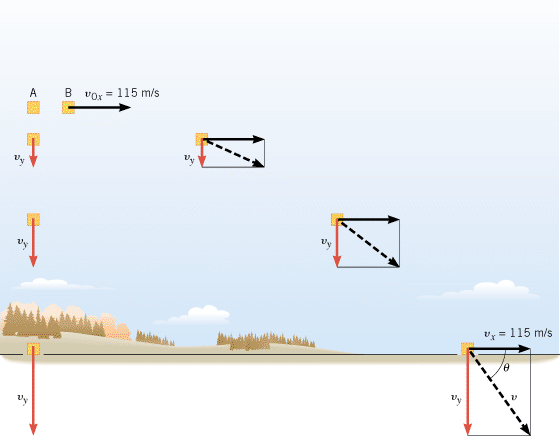
So if the package starts with the vertical component of its velocity, `v_(0y)`, equal to `"0 m s"^(-1)`, and since the gravitational acceleration is accelerating the package towards the ground, you can say that you have

`h = overbrace(v_(0y) * t)^(color(blue)(= 0 )) + 1/2 * g * t^2`

`h = 1/2 * g * t^2`

If you take `g = "9.81 m s"^(-2)`, you can say that the package fell from a height of

`h = 1/2 * "9.81 m s"^(-2) * ("9 s")^2`

`h = 1/2 * "9.81 m" color(red)(cancel(color(black)("s"^(-2)))) * 81 color(red)(cancel(color(black)("s"^2)))`

`h = "397.3 m"`

Since you only have one significant figure for the time needed for the package to hit the ground, you should round the answer to one significant figure and say that

`color(darkgreen)(ul(color(black)(h = "400 m")))`