What are the most probable velocity and the average velocity for a system that follows the Maxwell-Boltzmann distribution?
1 Answer
Dec 30, 2017
Maxwell Speed Distribution plot and typical speeds are given below in the figure.
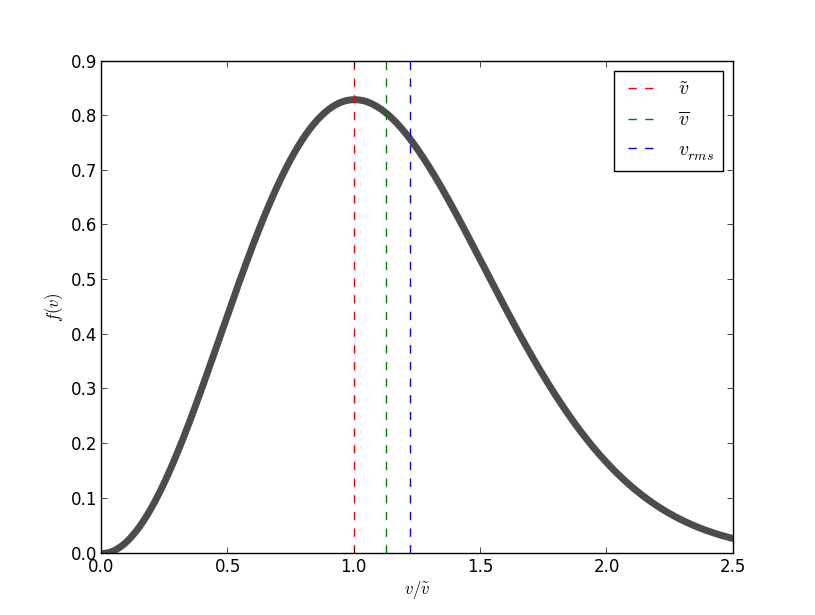
When a gaseous system is in thermal equilibrium, we can use Maxwell-Boltzmann statistics which gives us the probability of particle being in an energy state at a particular temperature.
There are three ways to quantify typical velocities of a distribution of particles in thermal equilibrium.
- The first typical velocity is the easiest to calculate and termed as the most probable velocity
#\tilde {v}# . The velocity at the top of the curve is the most probable velocity as the largest number of molecules have this velocity. To calculate this we set the first derivative with respect to velocity#v# of function#f(v)# equal to#0# .
In the plot above it is shown with red dotted line. - The second is the mean velocity or average velocity,
#barv# . Average Velocity is displacement over total time. We calculate the expectation value of#v# #barv=int_0^oo f(v)vdv#
It can be shown as#barv# is slightly greater than the most probably velocity#\tilde {v}# .
This is indicated as green dotted line. - The third is the root mean square velocity
#v_(rms)# , (included for sake of completeness). It is defined through the expression#v_(rms)^2-=bar(v^2)=int_0^oo f(v)v^2dv#
It can be shown as that root mean square velocity is greater than both the other two velocities.
This is depicted as blue dotted line.
