Question #be4c4

1 Answer
Ernest Z.
Jan 6, 2018

Warning! Long Answer. Usually, we titrate an amino acid to get information about its acid-base properties.

Explanation:

The formula of alanine is often written as #"H"_2"NCH"("CH"_3)"COOH"#, although it exists in ionic forms in solution.

Alanine has two dissociation steps.

#bb((1))color(white)(m)"H"_3stackrel("+")("N")"CH"("CH"_3)"COOH"+ "H"_2"O" ⇌ underbrace("H"_3stackrel("+")("N")"CH"("CH"_3)"COO"^"-")_color(red)("a zwitterion") + "H"_3"O"^"+"; "p"K_text(a₁)#

#bb((2))color(white)(m)"H"_3stackrel("+")("N")"CH"("CH"_3)"COO"^"-" + "H"_2"O" ⇌ "H"_3"NCH"("CH"_3)"COO"^"-" + "H"_3"O"^"+"; "p"K_text(a₂)#

The "neutral" form, which has one positive and one negative charge, is called a zwitterion (double ion).

Fron the titration curve, we can deduce the values of

  • #"p"K_text(a₁)#
  • #"p"K_text(a₂)#
  • #"pI"#, the isoelectric point, i.e. the pH at which the alanine exists mainly as a zwitterion

Here is a schematic titration curve for alanine.

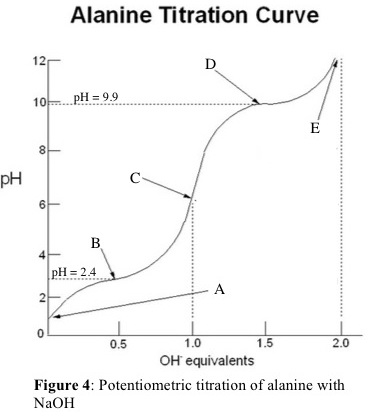
Alanine
(Adapted from Chegg)

Some points to note from the curve are:

(a) The graph has two "waves", showing that we have a diprotic acid.

(b) The two equivalence points occur after adding 1 eq of base (Point C) and 2 eq of base (Point E).

(c) The alanine is fully protonated at pH 1 (Point A), where it exists as a cation.

(d) After adding 0.5 eq base (Point B), we have deprotonated half of the carboxyl groups. At this point, #"pH = "p"K_text(a₁) = 2.34#.

(e) After adding 1 eq base (Point C), we have reached the first equivalence point and deprotonated all of the carboxyl groups. The alanine now exists primarily as a zwitterion, with no net charge.

(f) After adding 1.5 eq base (Point D), we have deprotonated half of the ammonium groups. At this point, #"pH = "p"K_text(a₂) = 9.69#.

(g) After adding 2 eq base (Point E), we have reached the second equivalence point and deprotonated all of the carboxyl groups. The alanine now exists as an anion.

(h) Point C is the isoelectric point. Even though it may be difficult to measure the pH from the graph, we can calculate it from the relation

#"pI" = 1/2("p"K_text(a₁) + "p"K_text(a₂)) = 1/2(2.34 + 9.69) = 6.02#

Related questions
Impact of this question
2060 views around the world
You can reuse this answer
Creative Commons License