Question

How to expand (x^2−2y)^6 using the binomial theorem?

Answer 1

See a solution process below

Explanation:

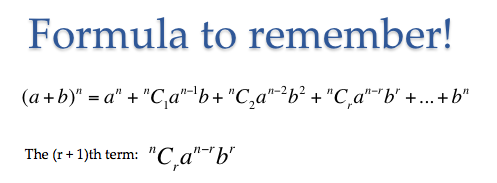
Here `color(white)(x)^n` `C_r=[n!]/{r!(n-r)!}`
Similarly you can do for any value of n and r except the negative ones , you will require to first make n(power to which it is raised) positive .

see below for solution
I am not using `color(white)(x)^n` `C_r=[n!]/{r!(n-r)!}` right now , i tried to use but in preview everything was messed , I think that would go a little difficult to understand . So , I'm using Pascal's Triangle .

Using this we get
`(x^2-2y)^6=(x^2)^6+6*(x^2)^5*(-2y)+15*(x^2)^4*(-2y)^2+20*(x^2)^3*(-2y)^3+15(x^2)^2*(-2y)^4+6*(x^2)*(-2y)^6`
Now only calculation part is left . I hope you will be able to do it .

If you face any difficulty then let me know in comments , i'll add calculation part .

You can view a similar question(with answer) here