Let's start with the skeleton equation:
#KClO_3 -> KCl + O_2#
Then, balance both sides:
#2KClO_3 -> 2KCl + 3O_2#
From this, we know that #2# moles of #KClO_3# corresponds to #3# moles of #O_2#. That means we just need to find out the number of moles of #O_2# in #"200g"# to see how many moles of #KClO_3# decomposed!
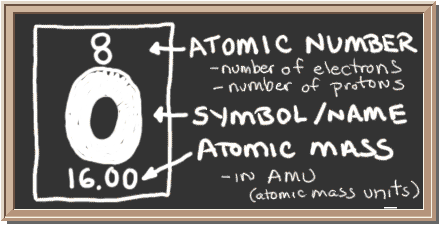
The mass of one mole, or the molar mass, of #O_2# is #16.00+16.00="32.00g"#, because the mass of one mole of #O# is #"16.00g"#.
So, #"200g"# of #O_2# is:
#200/32.00="6.25 moles"#
Again, #3# moles of #O_2# corresponds to #2# moles of #KClO_3#.
Therefore, #"6.25 moles"# of #O_2# corresponds to #2*6.25/3="4.16666667 moles"# of #KClO_3#.
Finally, because the question had #1# significant figure, our answer is #"4 moles"#.


