Question

Question #2e036

Answer 1

Shown by considering geometry...

Explanation:

I wanted to provide a simple way of evaluating this integral

The first thing we see is that the function is `y = sqrt(1-x^2)`

`=> y^2 = 1 - x^2`

`=> x^2+y^2 = 1`

This is just a circle of radius 1, and centre `(0,0)`

This is just this shaded region...

When evaluating from `x = 0` and `x=1`

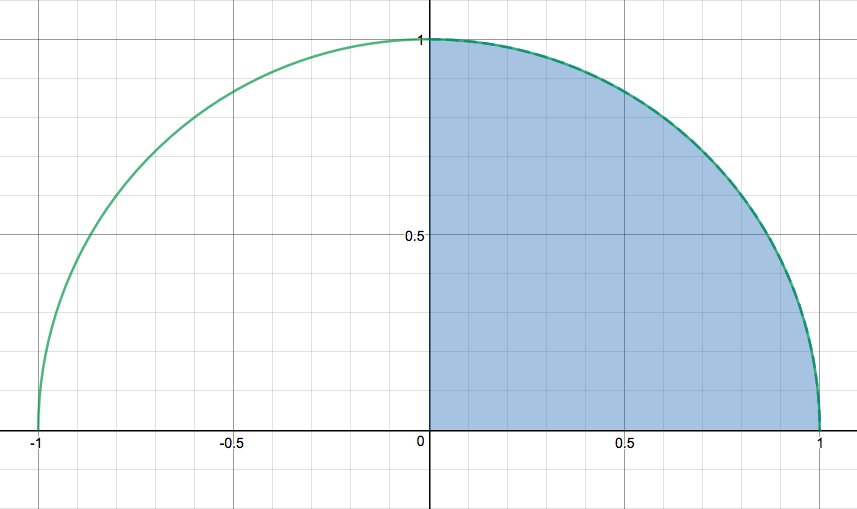
What is just a quarter of the area of a circle of radius 1

Full area of the circle = `= pir^2 =pi * 1^2 = pi`

Hence quarter area = `1/4 * pi`

`color(red)(= pi/4`

Answer 2

Conventoinal means of substitution...

Explanation:

The conventional way of solving this integral:

We can do a trigonometric substitution...

Let `x = sintheta`

`color(green)(dx = costheta d theta`

and we know `sin^2x + cos^2x = 1`

`=> costheta = sqrt(1-sin^2 theta )`

`=> color(blue)(costheta = sqrt(1-x^2)`

Hence our integral becomes:

`int color(blue)(costheta) color(green)(costheta d theta`

Changing the limits...

`theta = sin^(-1) x`

`x = 1 => theta = sin^(-1)(1) = pi/2`

`x = 0 => theta = sin^(-1)(0) = 0`

`=> int_0 ^(pi/2) cos^2 theta d theta`

Use `cos2theta = cos^2 theta - sin^2 theta`

`=> cos2theta = 2cos^2 theta -1`

`cos^2 theta = 1/2( cos2theta + 1 )`

`=>1/2 int_0 ^(pi/2) cos2theta + 1 d theta`

`=> 1/2[ 1/2 sin2theta + theta ]_0 ^(pi/2)`

`=> 1/2[ {0 + pi/2}-{0 + 0 } ]`

`color(blue)( = pi/4 )`