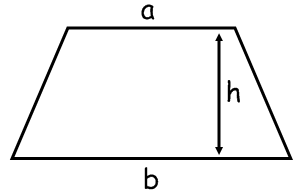
#"Example Problems"#
i) Find an expression for length #b# of this trapezium in terms of #A, a# and #h# (Harder)
ii) The trapezium above has length #a=3m# and a perpendicular height of #2m#. It has an area of #20m^2# Find the length #b#.(Easier)
iii) Given that #b=a+2x#, find the length #l# and the angle #theta# as on the diagram. (Harder - involves trigonometry)
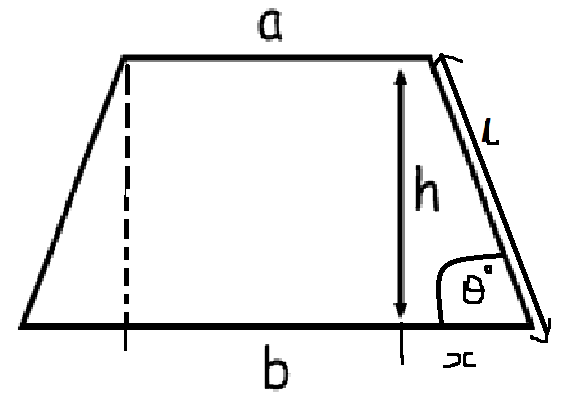
Give these problems a go, then read on for the answer.
Start:
i)
#A=1/2(a+b)*h#
#2A=h(a+b)#
#(2A)/h=a+b#
#(2A)/h-a=b#
We can tidy this up to:
#(2A-ah)/h=b#
ii) We have: #A=20, h=2, a=3#
From this step, just sub these values in.
#b=(2xx20-3xx2)/2#
#b=(cancel2(20-3))/cancel2#
#b=17m#
Even if you couldn't rearrange, you can still solve this:
#20=cancel(1/2)(b+3)xxcancel2#
(These numbers are really convenient)
#20=b+3#
#b=17m#
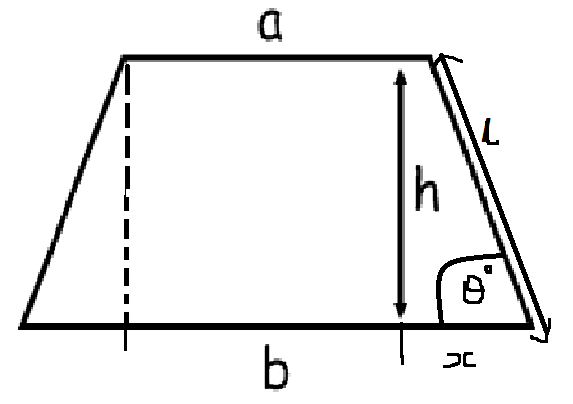
iii)
#b=a+2x#
#x=(b-a)/2#
#x=(17-3)/2#
#x=14/2=7#
Find #l# using Pythagoras' Theorem:
#x^2+h^2=l^2#
#l=sqrt(7^2+2^2)#
#l=sqrt53#
From our SOH CAH TOA, we can find #theta# using the #tan# function.
#tantheta=(O)/A#
#tantheta=h/x#
#tantheta=2/7#
#theta=15.95^@#
Proof of the formula
Sometimes it can help to have the proof so you can understand that this formula wasn't plucked out of thin air. You don't need to understand the proof, but its interesting nonetheless.
Consider this version of the above diagram.
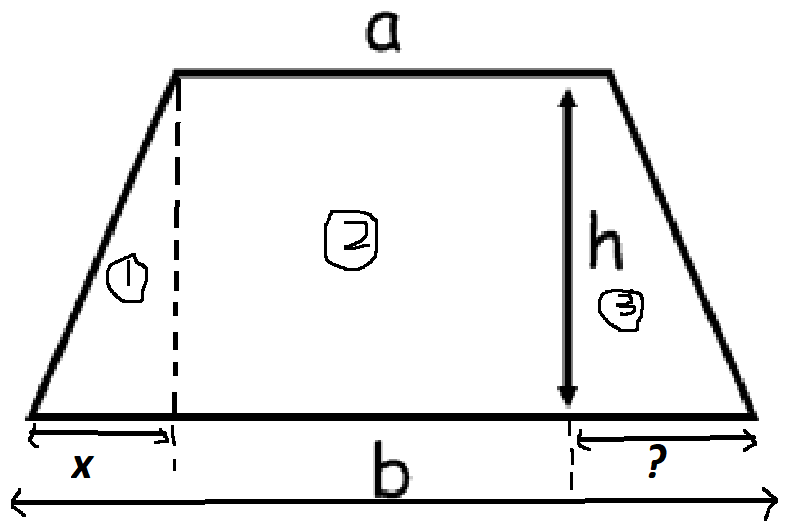
We have length #x# on the left and #?# on the right. Each region is called #(1), (2),# and #(3)#.
#"Let " A="area of trapezium"#
#A=(1)+(2)+(3)# where the number is the area of that region.
#(2)=ah# since this is rectangle, area=base*height.
#(1)=1/2xh# area of a triangle; 1/2baseheight.
For (3), we need to find an expression for #?# (this is why I didn't give this variable a name).
#b=x+a+?#
#?=b-x-a#
Therefore;
#(3)=1/2h(b-x-a)#
#=1/2bh-1/2xh-1/2ah#
Since we now have #(1), (2)# and #(3)#, we can find #A#.
#A=color(red)(1/2xh)+ah+1/2bh-color(red)(1/2xh)-1/2ah#
#A=1/2bh+ah-1/2ah#
#A=1/2ah+1/2bh#
#A=1/2(a+b)*h#