Question

Question #7261e

Answer 1

The slope of the line representing the acceleration as a function of the position is the negative ratio of the spring constant to the mass of the object.

Explanation:

The acceleration of an object is caused by a force applied to it. In a spring-mass system, the force is applied by the spring and is proportional to the distance from the rest position. So the acceleration as a function of position must be related to the spring constant. Let's find out by writing out some of the relevant equations. First, Newton's second law:

`F=ma -> a = F/m`

Next Hooke's law for the spring, remembering that the force opposes the displacement, `x`, trying to pull the mass back to rest

`F = -kx`

Combining these two we have:

`a = -k/m*x`

If we think of this as the equation of a line then the slope is just the factor in front of `x` (or take the derivative with respect to `x`):

`slope = -k/m`

Therefore, the slope of the line representing the acceleration as a function of the position is the negative ratio of the spring constant to the mass of the object.

Bonus: A quick test of this is to plot the relevant parameters vs. time where for simplicity, let's let the amplitude, `A=1`, and the angular frequency, `\omega=1`

`x = cos(t)`

then

`v = d/dt x = -sin(t)`

`a = d/dt v = -cos(t)`

We can make a table of the position, velocity and acceleration vs time (shown in part here):

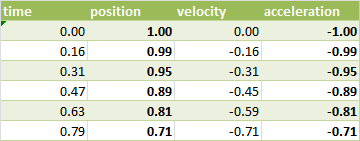
And then graph all of these vs. time:

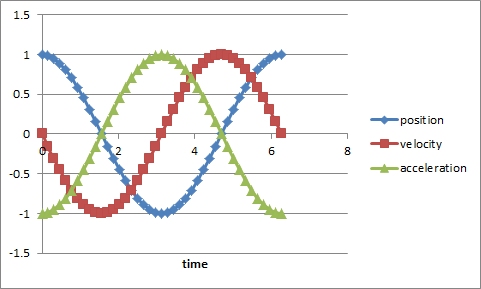
finally, we can select the position and acceleration columns and plot them on a graph:

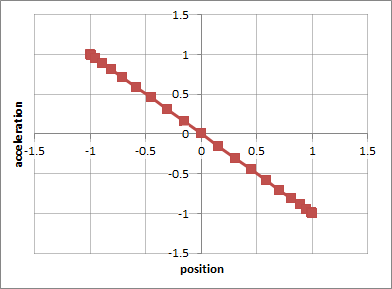
As we expected, this is a straight line with a negative slope. Notice that the points are not evenly spaced? It's because this is a parametric graph - each point represents a point in time where the points in time are evenly spaced. Since the mass is moving more quickly near the rest position, `x=0`, the points there are more spaced out. Also, the line only extends as far as the amplitude of the oscillation.