Question #05248
1 Answer
Feb 6, 2018
In point-slope form:
In slope intercept form:
Explanation:
We'll begin by finding
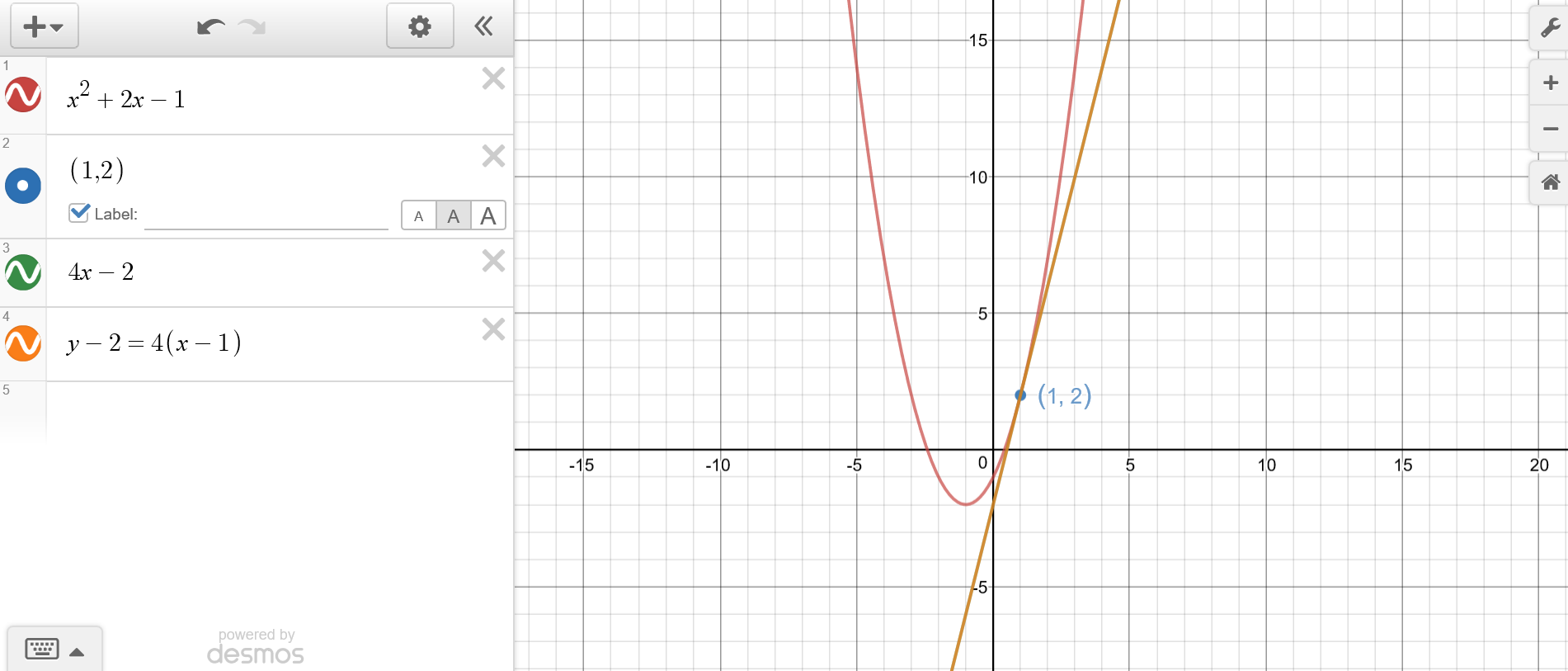
Given
Then
Next we evaluate the derivative at given
So
So the slope of the tangent line is
Now that we have the slope
So we substitute the known values and we'll get the equation of the tangent line in point-slope form:
In slope intercept form the equation of the tangent line:
Here's a graph of the function along with its tangent line at