Question #9ed95
1 Answer
Explanation:
By inspection you can see that
If we rearrange we get
Knowing that
Dividing we have:
So we can say that:
so
is equivalent to
We already known
The only solution is
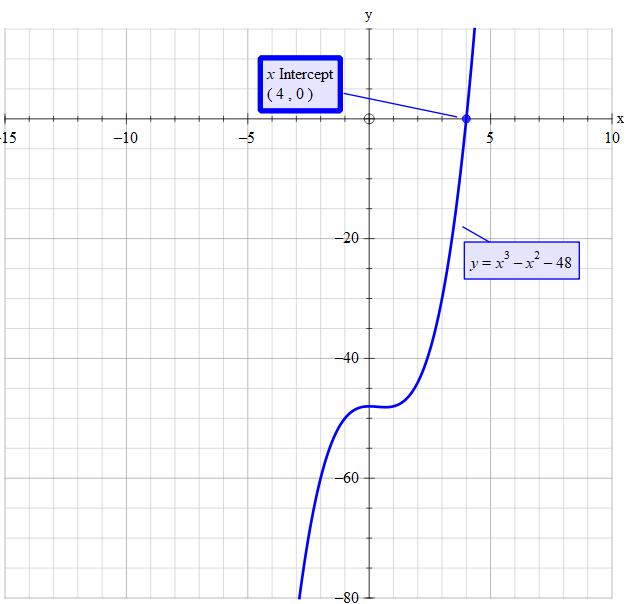
By inspection you can see that
If we rearrange we get
Knowing that
Dividing we have:
So we can say that:
so
is equivalent to
We already known
The only solution is
