Question

Question #69623

Answer 1

`x`-component is `=-21.65` Meters

`y`-component is `=-12.5` Meters

Explanation:

.

`OA` represents the displacement.

`OB` represents the `x` component of this displacement.

`BA` represents the `y` component of it.

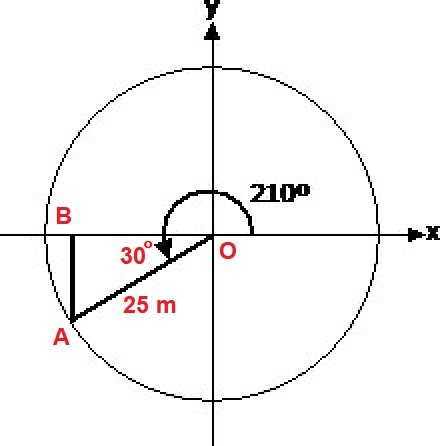
In the right triangle `Delta OAB`,:

`sin/_AOB=sin210^@=-sin30^@=(BA)/(OA)=(BA)/25=-1/2`

`BA=-25/2=-12.5` Meters

`cos/_AOB=cos210^@=-cos30^@=(OB)/(OA)=(OB)/25=-sqrt3/2`

`OB=-(25sqrt3)/2=-21.65` Meters

Answer 2

The x-component `= -21.65 m` and the y-component `= -12.5 m`.

Explanation:

OK. I will walk you thru how to do this. Draw x and y axes. Off to the right, along the x axis, is zero degrees. The direction 210 from the x axis is 210 degrees, counterclockwise from the x axis. Click this link to see a picture

Add a line on your x-y axes from the origin like the red line on the website that the link brought up. The inner blue arc is a `210^@` arc. If that arc had gone only to the -x axis, that would be `180^@`. Therefore the angle between the -x axis and the line you added for `210^@` is a `30^@` angle.

Now, put your trigonometry skills to work. Let the line you drew have a length of 25 m. From the end of that 25 m line, draw a line to the -x axis, parallel to the -y axis. Including the -x axis, you have a right triangle. We established at the end of the previous paragraph that the most acute angle of that triangle is a `30^@` angle. Using your trigonometry skills, what is the length of the side of the triangle along the x axis? (Ignore for now that this is in the negative x direction.)

I got `25 m*cos30^@ = 21.65 m`

Now, let's do that with the angle being `210^@`.

`25 m*cos210^@ = -21.65 m`

So, using `210^@` as the angle gives you the answer to the question "what is the x component of that displacement?"

Using that process, the y component of that displacement is

`25 m*sin210^@ = -12.5 m`

I hope this helps,
Steve