Question

Question #a254f

Answer 1

It should be `d/dx(sin^-1x) = 1/sqrt(1-x^2)`

Explanation:

`y = sin^-1x` so `sin y = x`.

Now use implicit differentiation to get

`dy/dx = 1/cosy`

and use trigonmetry to get

`= 1/sqrt(1-x^2)`

Answer 2

A more visual yet same as the answer below

Explanation:

`y=sin^-1(x)<=>sin(y)=x`

`sin(y)=x`

Create a triangle where `sin(y)=x/1`

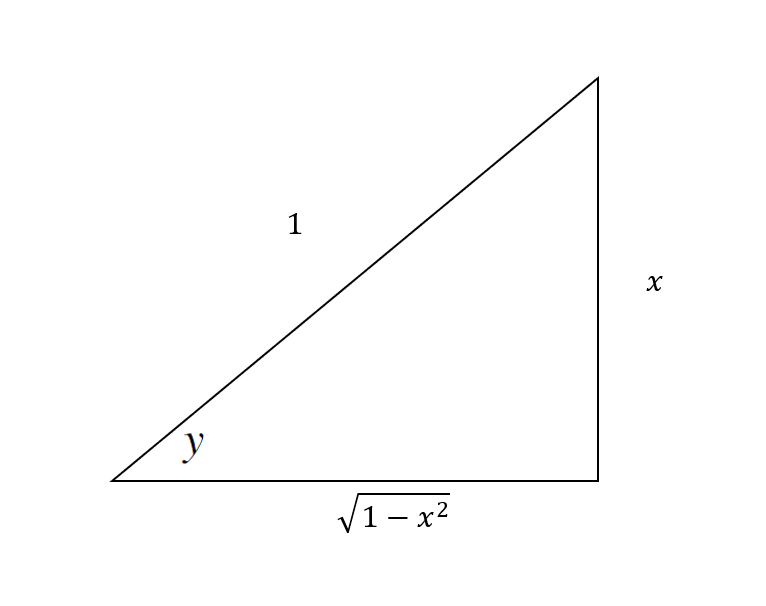
The missing side can be found using Pythagorean's Theorem

Differentiate both sides implicitly (W.R.T. `x`)

`dy/dx*cos(y)=1`

Divide `cos(y)` from both sides

`dy/dx=1/cos(y)`

Rewrite in terms of `x`

Since `sin(y)=x/1`

Then `cos(y)=sqrt(1-x^2)/1=sqrt(1-x^2)larr` Based on triangle

So `dy/dx=1/cos(y)=1/sqrt(1-x^2)`

`:.dy/dx[arcsin(x)]=1/sqrt(1-x^2)`