Question

6 equal circular discs placed so that their centres lie on the circumference of a given circle with radius (r), and each disc touches its 2 neighbours. What is the radius of a 7th disc placed in the centre which will touch each of the each existing ones?

Also what is the length of the exterior perimeter of the 6 discs?

Answer 1

Radius of `7^"th"` disc = `r/2`

Perimeter of each outer disc = `pir`

Explanation:

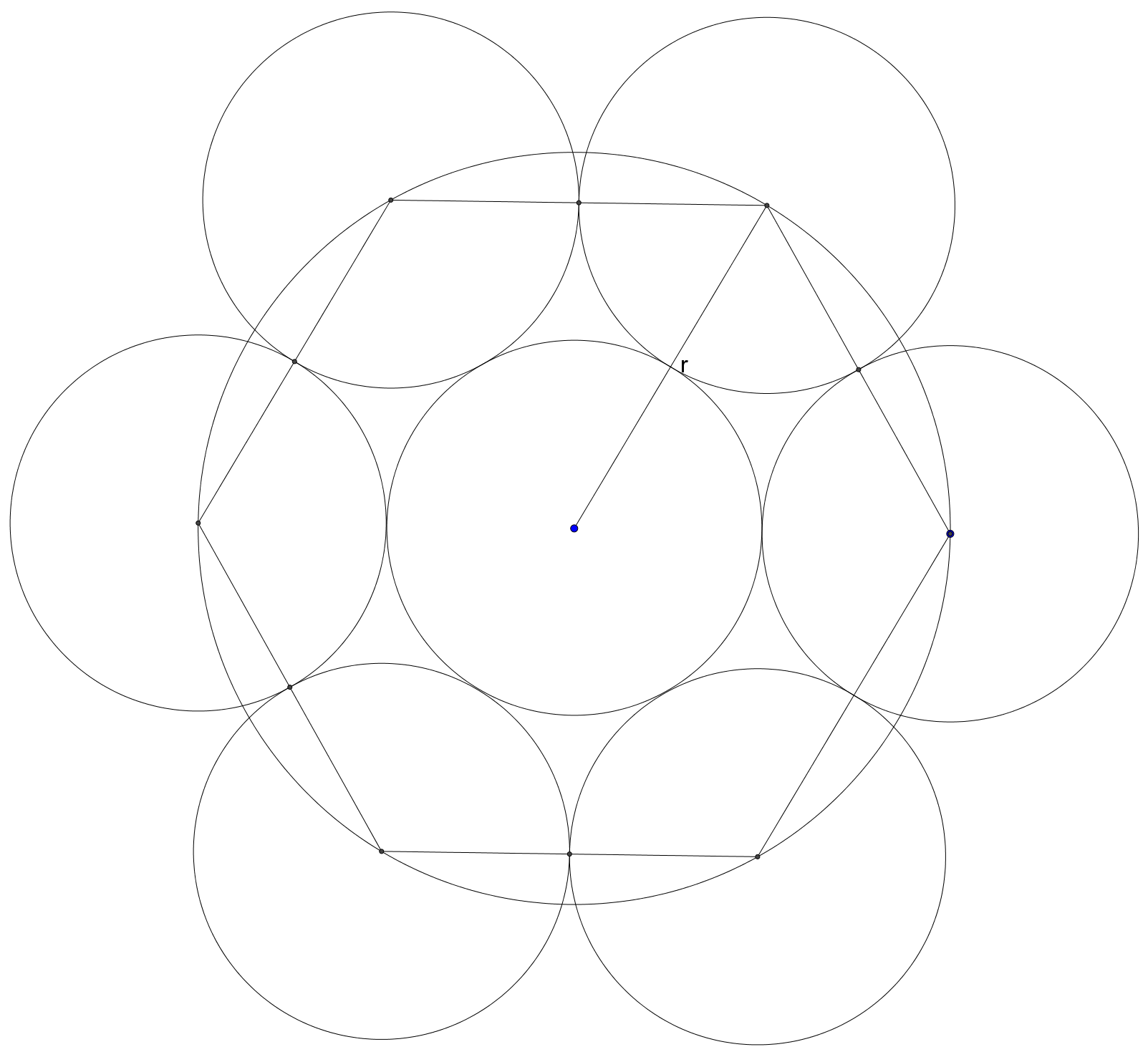
If we sketch a picture of the situation, we can see that the centers of the six discs lie on the vertices of a regular hexagon inscribed in the circle.

As the triangles formed by connecting the vertices of the hexagon to its center are equilateral, we know that the sides of the hexagon are also of length `r`.

As the sides of the hexagons serve as distances between the centers of the discs, we know each disc must intersect at a midpoint of a side, meaning each disc has a radius of `r/2`.

Given that the discs each have radius `r/2` and are centered at a distance of `r` from the center, then the `7^"th"` disc must also have a radius of `r/2` to touch each of the surrounding discs.

Finally, the perimeter of each of the outside discs is given by the product of twice its radius and `pi`. As they each have a radius of `r/2`, they each have a perimeter of `pir`