8m, 200N uniform ladder rests against a smooth wall. μs beetween the ladder and the ground is 0.6 and the ladder makes a 50° angle with the ground.how far up the ladder can an 80N person climb before the ladder begins to slip?
1 Answer
Mar 21, 2016
We need to consider the moment of the forces about a point (see diagram)
Explanation:
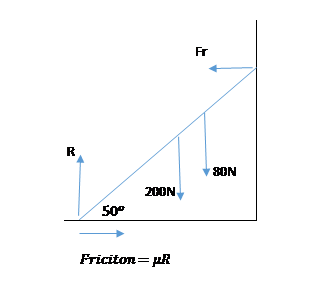
For the system to be in equilibrium in the diagram:
-
the horizontal forces must be in balance
-
the vertical forces must be in balance; and
- the clockwise moments about a point must equal the anticlockwise moments
Hence for
- Fr (reaction force with wall) = Friction force =
muR - R (normal reaction of ladder with ground= 200N+80N =280N
Hence
We will define the man as being
If we take moments about the point where the ladder touches the ground:
solving for
Might need checking!

