9/16x^2+7.5x=−25?
2 Answers
Mar 8, 2018
By moving the -25 to the left-hand side of the equation, one can factor the formula to get x, which is
Explanation:
Based on the fact that 9/16 and 25 have clean square roots (3/4 and 5, respectively) it occurred to me that the equation factored as such:
Using the factored version,
Mar 8, 2018
-20
Explanation:
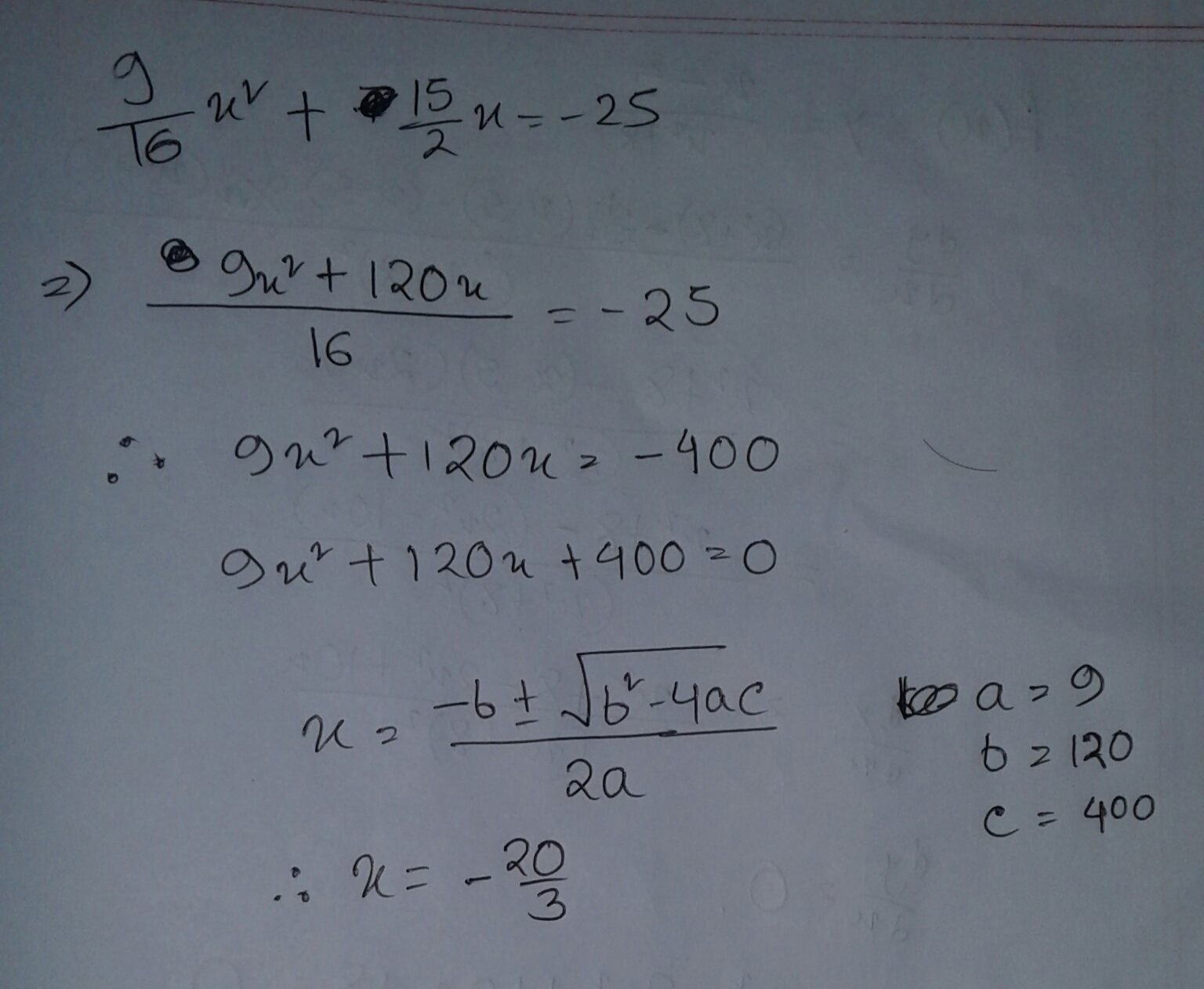
Simply solved the equation by the formula


