Question

A 1000kg car, travelling east at 30.0m/s, collides with a 3000kg truck, travelling north. After the collision, the vehicles stick together and the combined wreckage moves at 55.0◦ north of east. (a) What is the speed of the truck before the collision?

(b) What percentage of the initial kinetic energy of the system is lost during the collision?

Answer 1

(a) `approx 14.28ms^-1` North
(b) `approx 54.7` %

Explanation:

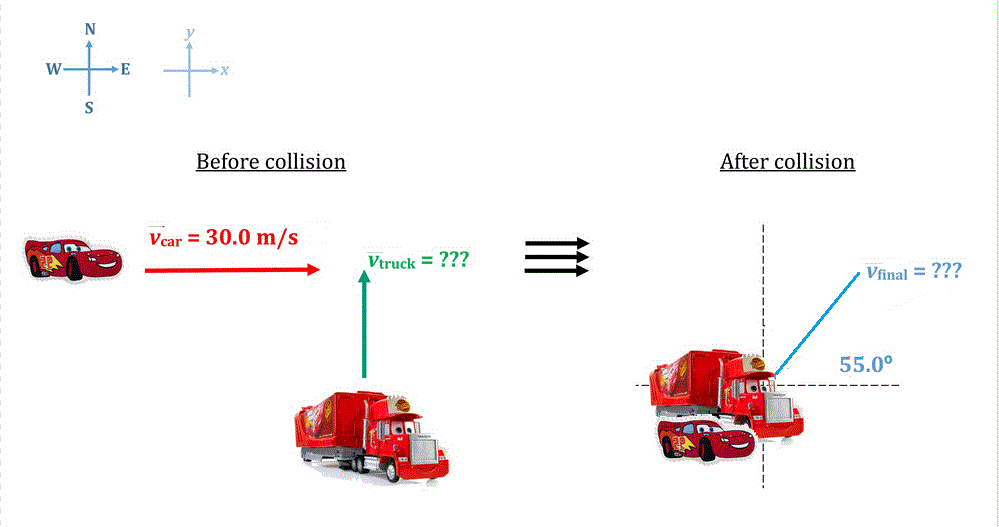
(a) For all collisions where no external forces are involved, the linear momentum

`vec p = m cdot vec v`

is conserved.

Let the car move along the `x` axis before the collision. Therefore truck moves along the `y` axis before the collision. Initial momentum is

`vecp_(i nitial)=m_(car)cdot v_(car)+m_(truck)cdot v_(truck)`
`=1000cdot 30.0hatx+3000cdot v_(truck)haty`

After the collision both (combined wreckage) move at `55.0^@` north of east with velocity `v_"final"`. Equating the `xand y` components of momentum we obtain
From `x` component
`1000cdot 30.0=4000cdot v_"final" cos55`
`v_"final"= (1000cdot 30.0)/(4000cdot0.57358)approx13.08ms^-1`

From `y` component
`3000cdot v_(truck)=4000v_"final" sin55`

`v_(truck)=(4000v_"final" sin55)/(3000)`

`=(4000cdot 13.08cdot 0.81915)/(3000)approx 14.28ms^-1` North

--.-.-.-.-.-.-..-.-.-.-.-.-.-.-.-..-.-.-.-.-.-.-.-.-.-
(b) Kinetic energy before collision

`KE_"before" = KE_"car" + KE_"truck"`
`= 1/2 cdot m_"car" cdot v_"car"^2 + 1/2 cdot m_"truck" cdot v_"truck"^2`
`= 1/2 cdot 1000 cdot 30.0^2 + 1/2 cdot 3000 cdot 14.28^2`
`= 755 877.6 J`

Kinetic energy after collision

`KE_"after" = 1/2 cdot (m_"car" + m_"truck") cdot v_"final"^2`

`= 1/2 cdot 4000 cdot 13.08^2`

`= 342172.8 J`

Now

`KE_"lost"=K_"before"-KE_"after" = 755877.6 -342172.8=413704.8J`
% `KE_"lost" =413704.8/ 755877.6xx100approx 54.7`