A 42-gram weight and a 18-gram weight are placed on opposite sides of a beam, each at a distance of 15 centimeters from the fulcrum. Where should a 60-gram weight be placed to balance the beam?
1 Answer
The 60g loading should be placed between the 18g loading and the fulcrum. Which is
Explanation:
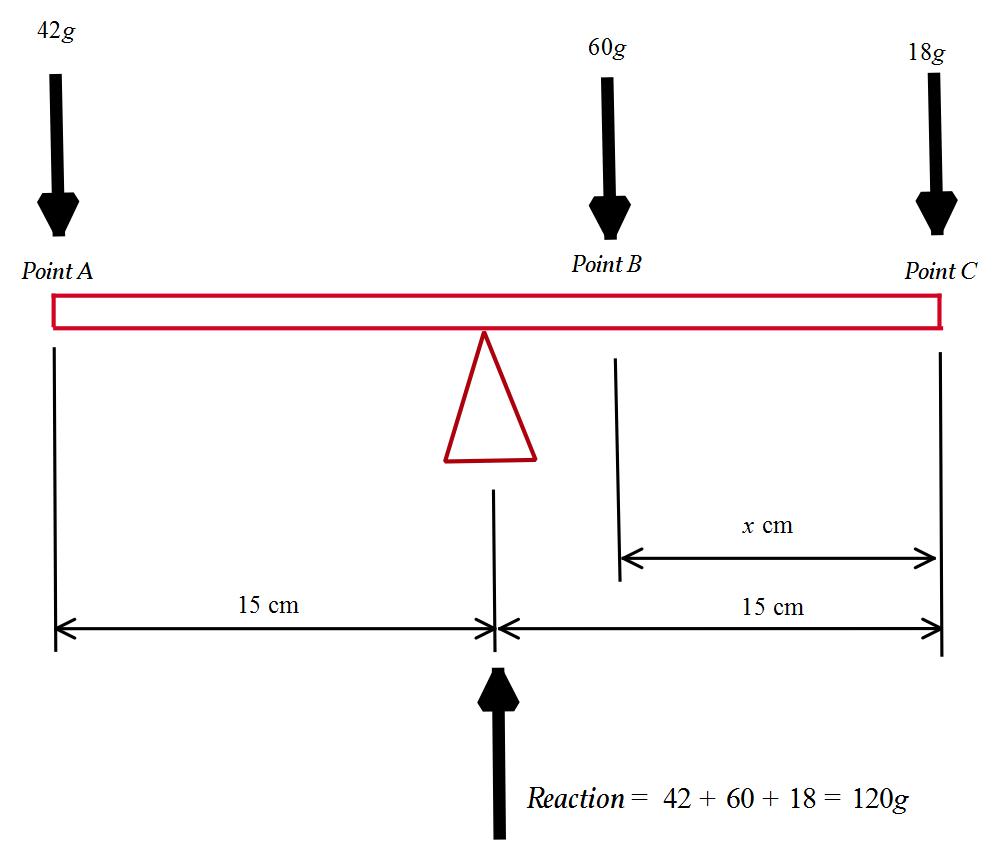
NOTE THAT: the 18 gram loading is not sufficient to maintain equilibrium with the 42 grams. So the addition loading must be placed on the 18 gram side of the beam.
Assumption 1: The beam is of uniform weight thus the weight
Assumption 2:The fulcrum is located centrally to the length of the
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let the reaction be R
A moment is the force times its distance to the point under consideration.
All moments must be in equilibrium (balanced) else the beam would be in motion.
The upward reaction of the support must equal the downward loading otherwise the system would fail and collapse.
Taking moments about point C
But the distance of point C to the point of moments is 0.
So
The 60g loading should be placed between the 18g loading and the fulcrum such that it is

