A 5.7 diameter horizontal pipe gradually narrows to 3.6 cm. The the water flows through this pipe at certain rate, the gauge pressure in these two sections is 32.5 kPa and 24.0 kPa, respectively. What is the volume of rate of flow?
1 Answer
The flow rate is
Explanation:
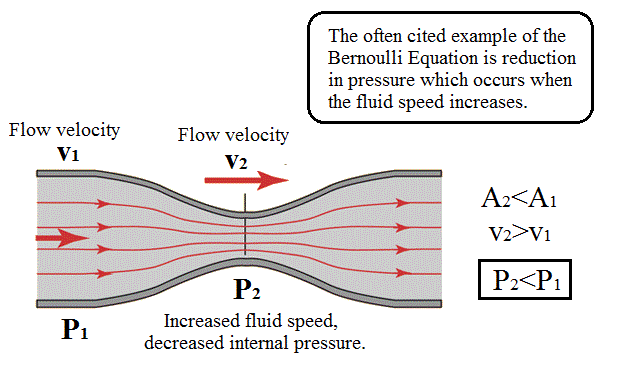
Apply Bernoulli's Principle
Since the Pipe is horizontal,
So,
The flow rate is constant
Where
Where
Therefore,
The pressures are
And the density of water is
Therefore,
Finally,
The flow rate is

