A 5 L5L container holds 15 15 mol and 6 6 mol of gasses A and B, respectively. Every three of molecules of gas B bind to two molecule of gas A and the reaction changes the temperature from 360K360K to 210K210K. By how much does the pressure change?
2 Answers
The pressure changed by
Explanation:
To get started we’ll work out how many moles of gas are present at the end of the reaction. There are 6 moles of gas B. In the reaction gas B bonds with gas A at a ratio of 3:2 molecules, so that ratio will apply to the number of moles also. 3 moles of gas B will bond with 2 moles of gas A. In total all 6 moles of gas B will bond with 4 moles of gas A and the product of that reaction will be 2 moles of a new gas. Let’s call the new gas, gas C.
That leaves us with 15 – 4 = 11 moles of gas A, 0 moles of gas B (it all reacted), and 2 moles of gas C. So the final number of moles of gas will be 13 moles. The initial number for moles was 15 + 6 = 21 moles.
Calculate the Final Pressure
To solve the problem of the pressure change we will use the ideal gas equation:
You may be familiar with the equation stated as:
Since the LHS of the equation is equal to a constant we can now state the equation like this:
The volume does not change so
The above equation will give us p₂ as a multiple of p₁. Now substitute the values into the equation:
Pressure Change
To calculate by how much the pressure changes find the difference between initial and final pressures:
Calculate the value of p₁ by using the ideal gas equation:
Volume conversion:
The pressure therefore changed by:
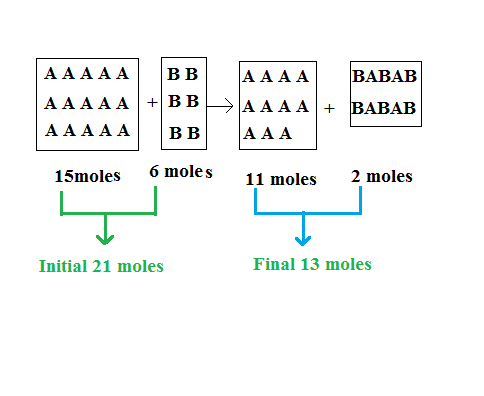
As explained in the above figure
Initial number of moles of gas molecules was
and Final number of moles of gas molecules was
We Know from Equation of state for ideal gas
PV = nRT ,
where:
- P = pressure in atm
- V = volume in L
- T = temperature in K
- n = number of moles
- R = universal gas constant.=0.082
LatmK^-1mol^-1
For Initial state
If pressure is
Volume
Number of moles
Temperature
and then
For Final state
If pressure is
Volume
Number of moles
Temperature
and then
So decrease in Pressure:
When we convert this to



