Question

A 60 N force acting at 30° east of north and a second 60 N force acting in the direction 60° east of north are concurrent forces. What is the resultant force?

What is the magnitude and direction of their equilibrant?

Answer 1

`"magnitude" = 116` `"N"`

`"direction" = 45^"o"` north of east

Explanation:

We're asked to find the magnitude and direction of the resultant force (which we'll call `vecR`) given two component forces.

To do this, we can first find the components of the two constituent forces, using the equations

`ul(F_x = Fcostheta`

`ul(F_y = Fsintheta`

where

• `F_x` is the `x`-component of the force

• `F_y` is the `y`-component of the force

• `F` is the magnitude of the force

• `theta` is the direction of the force (relative to the positive `x`-axis)

For the first force `vecF_1`, we have

• `F_1 = 60` `"N"`

• `theta_1 = 90^"o" - 30^"o" = ul(60^"o"`

The given angle was `30^"o"` east of north, and angles are typically measured from the positive `x`-axis toward the positive `y`-axis; i.e. from east to north.

Here's what I mean by that:

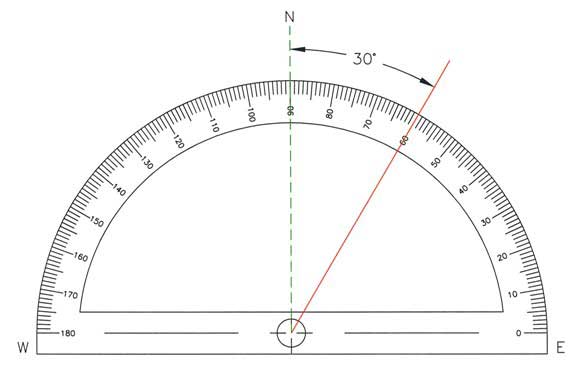
The angle measured from the positive `x`-axis is thus `60^"o"`.

Therefore, plugging in values, we have

`F_(1x) = F_1costheta_1 = (60color(white)(l)"N")cos(60^"o") = color(red)(30.0color(white)(l)"N"`

`F_(1y) = F_1sintheta_1 = (60color(white)(l)"N")sin(60^"o") = color(green)(52.0color(white)(l)"N"`

For the second force `vecF_2`, we have

• `F_2 = 60` `"N"`

• `theta_2 = 90^"o" - 60^"o" = ul(30^"o")color(white)(aal)` (same reason as before)

Therefore, we have

`F_(2x) = F_2costheta_2 = (60color(white)(l)"N")cos(30^"o") = color(red)(52.0color(white)(l)"N"`

`F_(2y) = F_2sintheta_2 = (60color(white)(l)"N")sin(30^"o") = color(green)(30.0color(white)(l)"N"`

`" "`

Now, let's find the sum of the respective components of these two force vectors (these will be the components of the resultant force):

`sumF_x = R_x = F_(1x) + F_(2x) = color(red)(30.0color(white)(l)"N") + color(red)(52.0color(white)(l)"N") = color(red)(ul(82.0color(white)(l)"N"`

`sumF_y = R_y = F_(1y) + F_(2y) = color(green)(52.0color(white)(l)"N") + color(green)(30.0color(white)(l)"N") = color(green)(ul(82.0color(white)(l)"N"`

The magnitude of the resultant force `vecR` is given by

`ul(R = sqrt((R_x)^2 + (R_y)^2)`

So

`R = sqrt((color(red)(82.0color(white)(l)"N"))^2 + (color(green)(82.0color(white)(l)"N"))^2) = color(blue)(ulbar(|stackrel(" ")(" "116color(white)(l)"N"" ")|)`

The direction of the resultant force is given by

`ul(tantheta = (R_y)/(R_x)`

Or

`ul(theta = arctan((R_y)/(R_x))`

So

`theta = arctan((color(green)(82.0color(white)(l)"N"))/(color(red)(82.0color(white)(l)"N"))) = color(blue)(ulbar(|stackrel(" ")(" "45^"o"" ")|)`

measured anticlockwise from the positive `x`-axis.