Question

A ball is launched vertically upwards from ground level with an initial velocity of 30 m/s. About how much time elapses before it reaches the ground? About what maximum altitude does it reach above ground? Please explain I'm so confused.

Answer 1

I found `6s` and `46m`

Explanation:

The ball starts with initial velocity `v_i=30m/s` and it reaches maximum height where the velocity will be zero, `v_f=0`. During the upwards bit the acceleration of gravity `g=9.8m/s^2` is slowing it down up to the maximum height where the ball finally stops;

You can say that the final velocity depends upon the initial velocity AND the contribution of the acceleration that operates for a certain time `t`, or:

`v_f=v_i+at`

in our case:
`0=30-9.8t` the acceleration is negative because it is directed downwards (see the diagram).
So you have that the time to reach the maximum height will then be:
`t=30/9.8=3s`.

This is the time to go up; you double it to consider also the second leg of the trip when the ball comes back to the ground: so:

`t_("tot")=2t=2*3=6s`

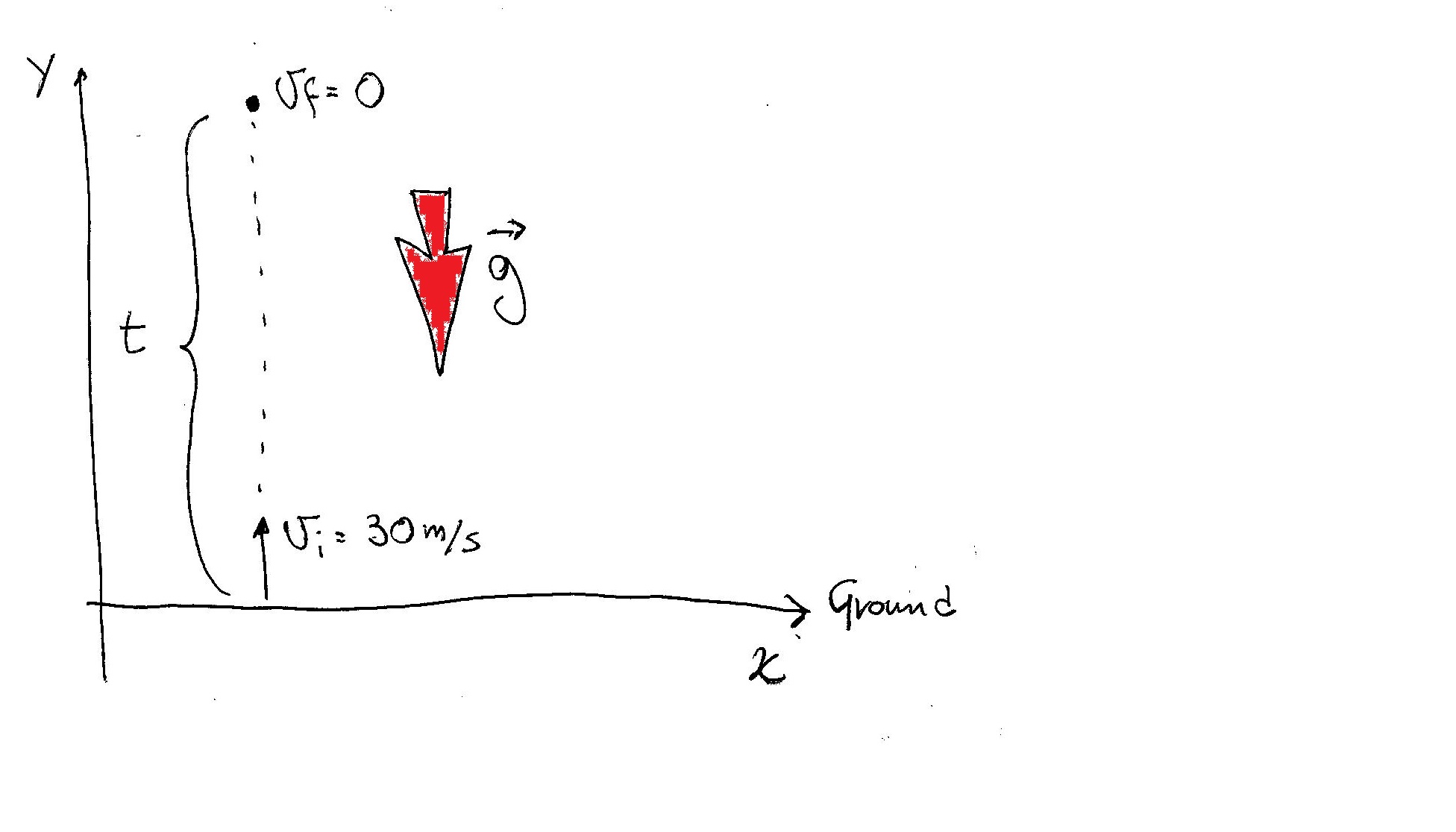
The maximum height can be found considering:
`y_f-y_i=v_it+1/2at^2`
with our data:
`y_f-0=30*3-1/2(9.8)(3)^2`
again the acceleration of gravity is directed downwards and we use the time to go up.
So:
`y_f=46m`