Question

A ball is thrown towards a cliff with an initial speed of 30.0 m/s directed at an angle of 60.0◦ above the horizontal. The ball lands on the edge of the cliff 4.00 s after it is thrown. ?

(a) What is the height of the cliff?
(b) What is the maximum height reached by the ball?
(c) What is the ball’s impact velocity?

Answer 1

(a)

`25.5"m"`

(b)

`34.4"m"`

(c)

`20.0"m/s"` at an angle to the vertical of `48.6^@`

Explanation:

(a)

Diagram (a) describes the scenario. (apologies for the artwork):

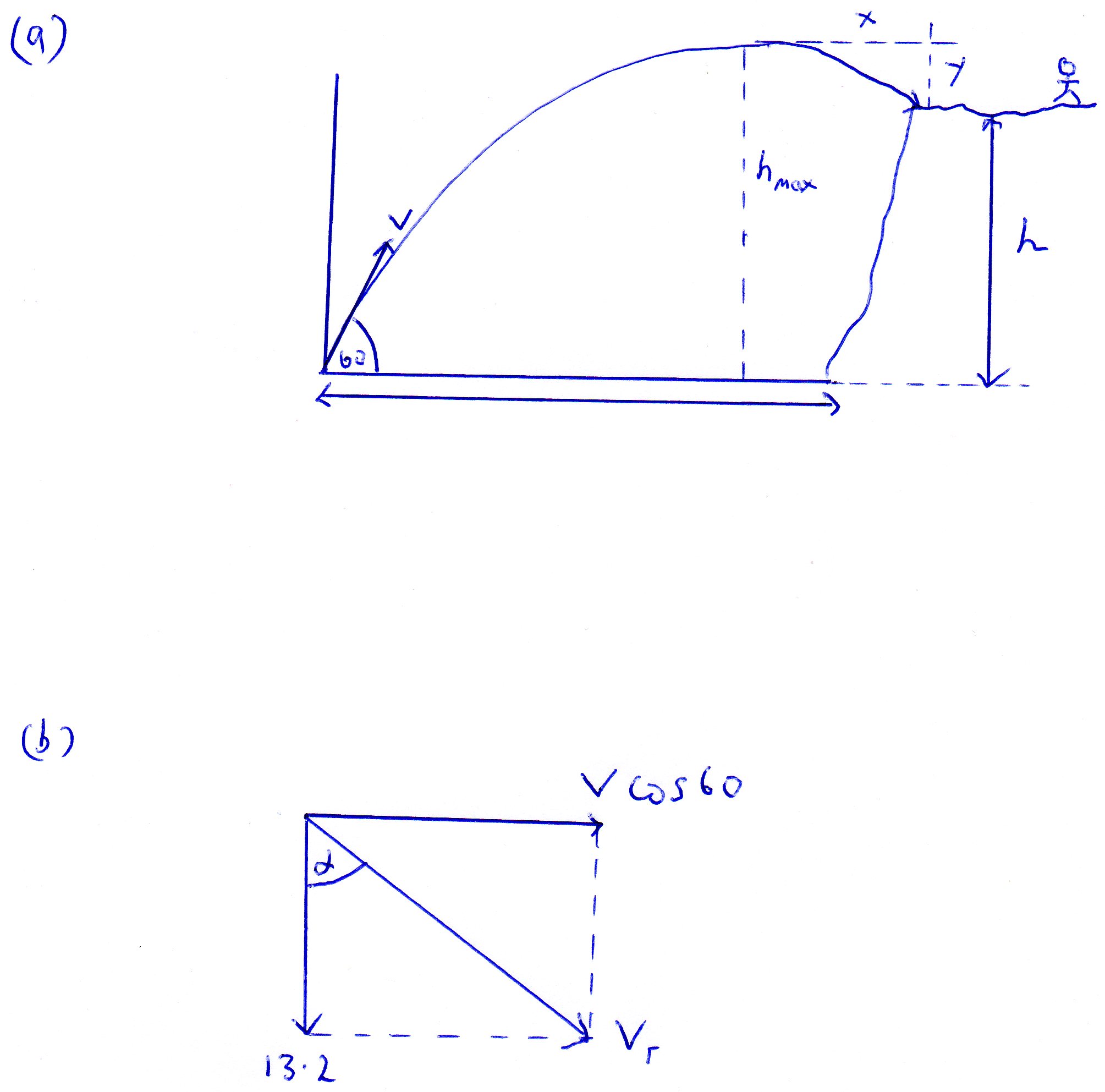
(a)

To get `h` we can use the equation of motion:

`s=ut+1/2at^2`

The vertical component of the initial velocity `v` is given by:

`u=vsin60`

So the expression for `h` becomes:

`h=vsin60t-1/2"g"t^2`

`:.h=30sin60xx4-0.5xx9.8xx4^2`

`:.h=103.9-78.4=25.5"m"`

(b)

To get the maximum height `h_(max)` we can use:

`v^2=u^2+2as`

This becomes:

`0=(vsin60)^2-2gh_(max)`

`:h_(max)=(30xx0.866)^2/(2xx9.8)`

`:.h=34.43"m"`

(c)

To get the vertical component `v_y` of the impact velocity we need to get the time it takes to go from the maximum height to the moment it hits the cliff.

In diagram (a) the distance travelled is marked "y".

This can be found from:

`y=h_(max)-h`

`:.y=34.43-25.5=8.9"m"`

So now we can say that;

`y=1/2"g"t^2`

`:.t=sqrt((2y)/(g)`

`:.t=sqrt((2xx8.9)/(9.8))=1.35"s"`

Now we can use:

`v=u+at`

This becomes:

`v_(y)=0+(9.8xx1.35)`

`:.v_(y)=13.2"m/s"`

Now we know the vertical and horizontal components of velocity we can find the resultant `v_r` by referring to diagram (b):

Using Pythagoras we can say that:

`v_(r)^2=13.2^2+(vcos60)^2`

`:.v_r^2=13.2^2+(30xx0.5)^2`

`v_r^2=399.24`

`:.v=20"m/s"`

If you want the angle you can say that:

`tanalpha=(vcos60)/13.2=(30xx0.5)/13.2=1.136`

From which `alpha=48.6^@`