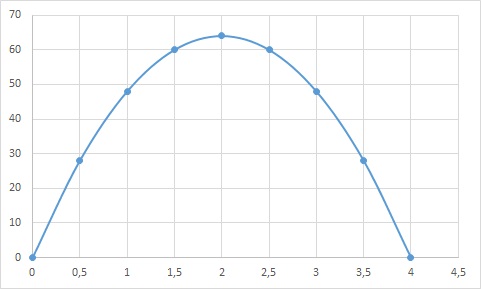
A ball is thrown vertically with an initial velocity of #64# feet per second. Its height above the ground after #t# seconds is given by #h(t) = 64t—16t^2#. What is the maximum height?
1 Answer
Nov 17, 2015
I found
Explanation:
Ok...probably you can do this differently but I would try to find the vertex of the parabola describing the trajectory:
1) derive it:
2) set derivative equal to zero:
3) use this value of
Graphically: