Question

A ball with a mass of `5 kg` is rolling at `2 m/s` and elastically collides with a resting ball with a mass of `2 kg`. What are the post-collision velocities of the balls?

Answer 1

`"velocities of objects after collision are:"`
`"the red ball's velocity :"v_1^'=6/7" "m/s" at positive direction"`
`"the blue ball's velocity :"v_2^'=20/7 " "m/s" at positive direction"`

Explanation:

`"let the velocities of objects after collision be "v_1' " and " v_2^'`

`P_1':" momentum of the red ball after collision"`
`v_1^':"velocity of the red ball after collision"`

`P_1^'=m_1*v_1^'`
`P_1^'=5*v_1^'`

`P_2^':"momentum of the blue ball after collision"`
`v_2^':"velocity of the blue ball after collision"`

`P_2^'=2*v_2^'`

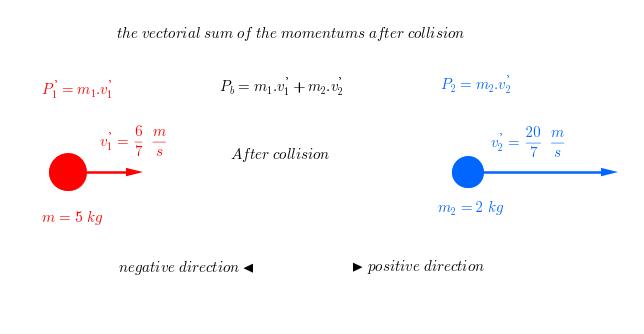
`"vectorial sum of the momentums after collision :"`
`P_a=P_1^'+P_2^'`
`P_a=5v_1^'+2v_2^'`

`P_b=P_a" conservation of momentum"`

`10=5v_1^'+2v_2^'" "(1)`

`"the total velocities of the objects must be equal"`

`v_1+v_1^'=v_2+v_2^'`

`2+v_1^'=0+v_2^'`

`color(red)(v_2^'=2+v_1^')" "(2)`

`"use (1)"`

`10=5v_1^'+2(color(red)(2+v_1^'))`

`10=5v_1^'+4+2v_1^'`

`10=7v_1^'+4`

`10-4=7v_1^'`

`6=7v_1^'`

`color(green)(v_1^'=6/7)" "m/s`

`"use (2)"`

`v_2^'=2+color(green)(6/7)`

`v_2^'=20/7" "m/s`