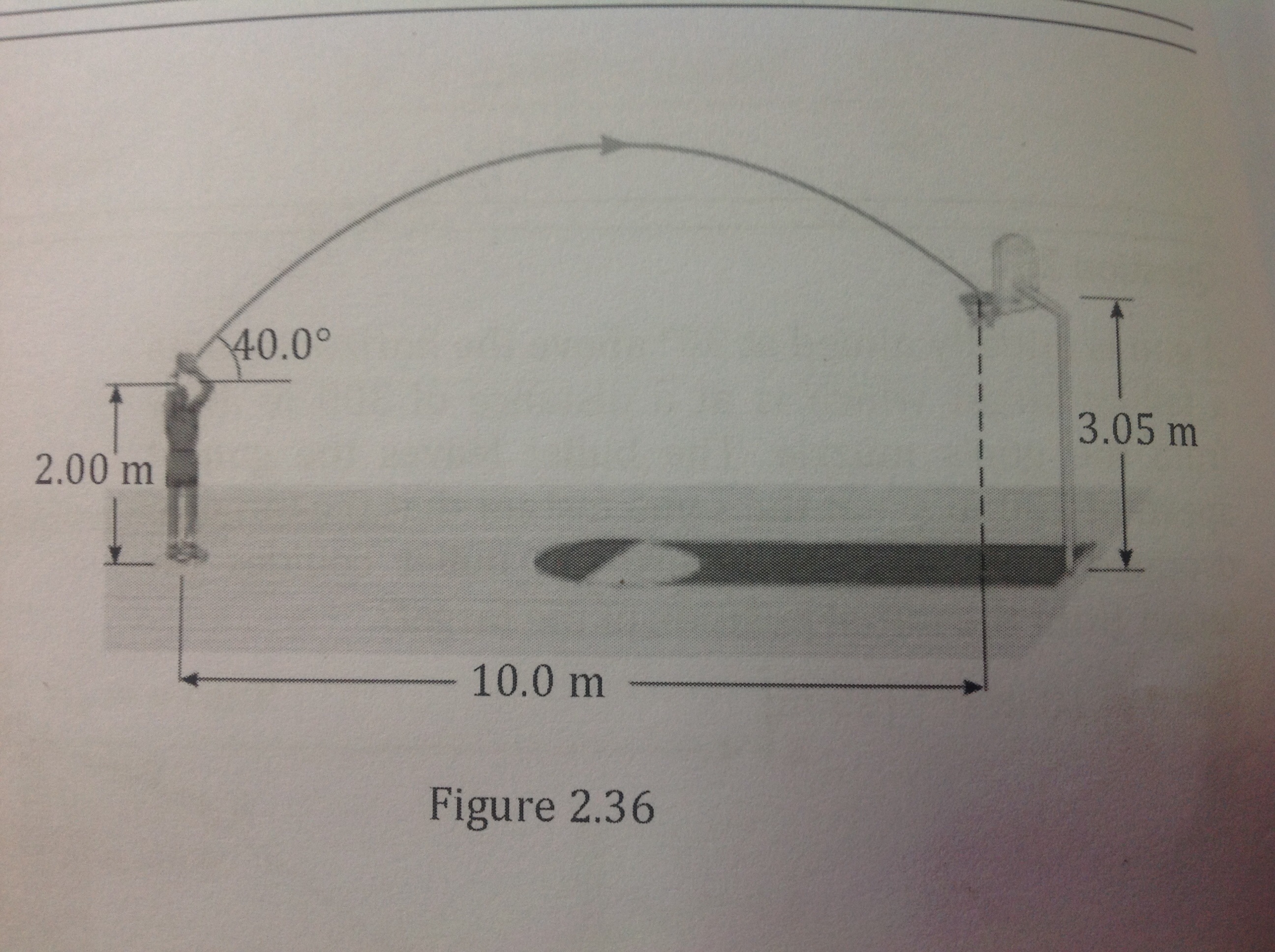
A basketball player who is 2m tall is standing on the floor 10m from the basket. The height of the basket is 3.05m. If he shoots the ball at an angle of 40degree with the horizontal ,at what initial speed must he throw so that it goes through the hoop??

Question

25213 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-28T09:43:27

The initial speed is #=10.7ms^-1#

Let the initial speed be #=ums^-1#

Resolving in the vertical direction #uarr^+#

We apply the equation of motion

#s=ut+1/2at^2#

#y=utsintheta-1/2g t^2#................#(1)#

Resolving in the horizontal direction #rarr^+#

We apply the equation of motion

#x=u(costheta) t#

#t=x/(ucostheta)#............................#(2)#

Plugging in the value of #t# in the equation #(1)#, we get

#y=usintheta*x/(ucostheta)-1/2g*(x/(ucostheta))^2#

Let the origin be the point where the ball is thrown

#3.05-2=10tan40-1/2*9.8*(10/(ucos40))^2#

#4.9*(10/(ucos40))^2=8.39-1.05=7.34#

#(10/(ucos40))=sqrt(7.34/4.9)=1.22#

#u=10/(1.22cos40)=10.7ms^-1#
graph{0.84x-0.073x^2 [-0.53, 15.274, -2.315, 5.585]}