Question

A block weighing `15 kg` is on a plane with an incline of `pi/3` and friction coefficient of `1/10`. How much force, if any, is necessary to keep the block from sliding down?

Answer 1

The force is `=134.7N`

Explanation:

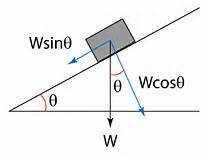
Resolving in the direction parallel to the plane `↗^+`

Let the force necessary to keep the block from sliding down be `=F`

The force of friction is `f_r=mu*N=mu*mgcostheta`

The component of the weight is `=mgsintheta`

Therefore,

`F=mumgcostheta+mgsintheta`

`=mg(mucostheta+sintheta)`

`=15g(1/10*cos(pi/3)+sin(pi/3))`

`=134.7N`

Answer 2

`F = 120` `"N"` up the incline.

Explanation:

I'll assume that `1/10` is the coefficient of static friction.

We're asked to find if any force is required (and if there is, what is it) to keep the block stationary and prevent it from sliding down.

We have our relationship for the friction force `f_s`, the coefficient of static friction `mu_s`, and normal force `n`:

`f_s <= mu_sn`

Here, `theta = pi/3`, and the mass of the block is `15` `"kg"`.

The normal force `n` is given by

`n = mgcostheta = (15color(white)(l)"kg")(9.81color(white)(l)"m/s"^2)cos(pi/3) = color(red)(73.6` `color(red)("N"`

The quantity `mu_sn` is thus equal to

`mu_sn = 1/10(color(red)(73.6color(white)(l)"N")) = 7.36` `"N"`

This represents the maximum static friction force that prevents the object from sliding.

Taking the positive `x`-direction down the incline, we have

`sumF_x = mgsintheta + (-f)`

`mgsintheta = (15color(white)(l)"kg")(9.81color(white)(l)"m/s"^2)sin(pi/3) = 127` `"N"`

Since this number is greater than the allowed static friction force of `7.36` `"N"`, a force is necessary to prevent the block from sliding.

This force is

`F = mgsintheta - f_s = 127` `"N"` `- 7.36` `"N"` `= color(blue)(120.` `color(blue)("N"`

directed up the incline.