A body starts from rest and is uniformly accelerated for 30 sec.The distance covered in first 10 sec is #x_1# , for next 10 sec is #x_2# and for last 10 sec is #x_3# the then the ratio of #X_1:X_2:X_3#=?
2 Answers
Apr 11, 2017
Explanation:
- please look at the animation and calculate the colored areas.
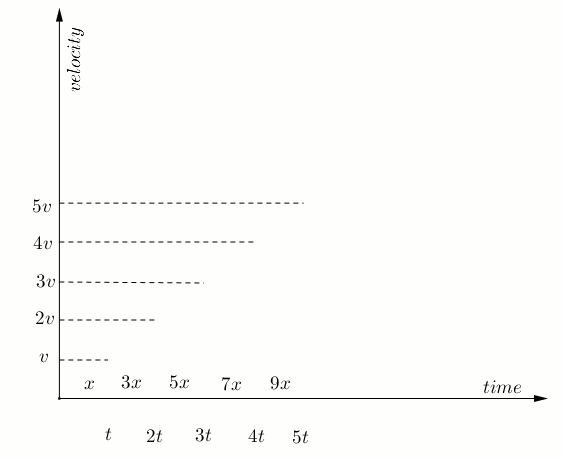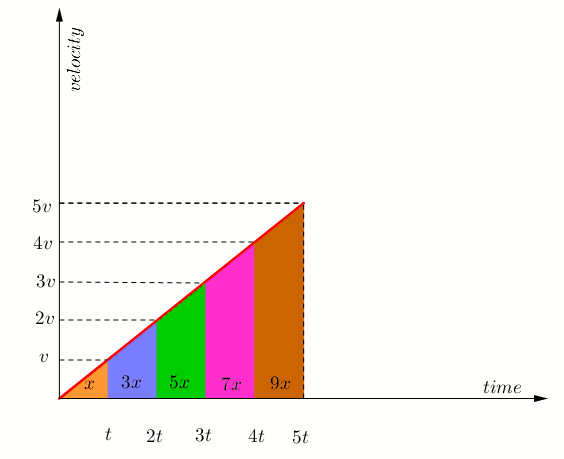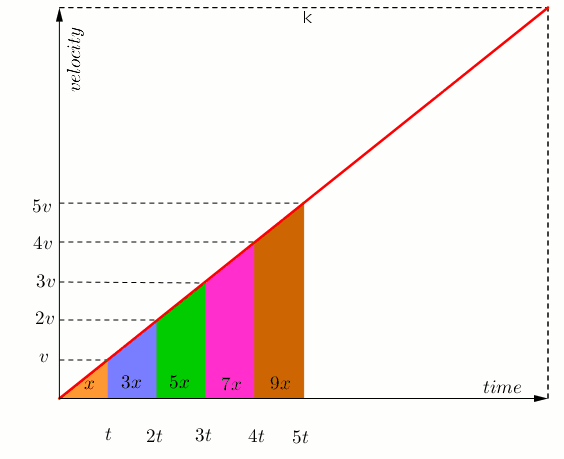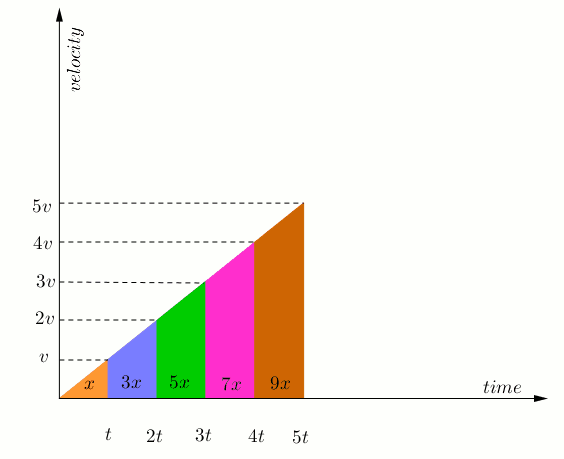
Apr 12, 2017
Explanation:
The applicable kinematic expression is
Distance traveled in first
Distance traveled in next
Distance traveled in last
the required ratio is

